An LCR series circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant ‘b’, the correct equivalence would be (Take, i = current, V = voltage, x = displacement, q = charge, F = force, v = velocity)
q↔x,v<↔>i,F↔V
q↔v,i↔x,F↔V
q↔x,v↔V,F→i
q↔F,i↔x,V→v
The correct Answer is:A
To solve the problem of comparing an LCR series circuit with a damped harmonic oscillator, we will derive the equations for both systems and establish the equivalences.
1. Write the Equation for a Damped Harmonic Oscillator:
The equation for a damped harmonic oscillator (spring-mass system) is given by:
md2xdt2+bdxdt+kx=0
Here, m is the mass, b is the damping constant, k is the spring constant, x is the displacement, and dxdt is the velocity.
Hint: Identify the terms in the equation: mass, damping, and restoring force.
2. Write the Equation for an LCR Series Circuit:
For an LCR circuit, applying Kirchhoff's voltage law gives:
Ldidt+Ri+qC=0
where L is the inductance, R is the resistance, C is the capacitance, i is the current, and q is the charge on the capacitor.
Hint: Recognize that the terms represent inductive, resistive, and capacitive effects.
3. Relate Current and Charge:
The current i is the rate of change of charge q:
i=dqdt
Substitute this into the LCR equation:
Ld2qdt2+Rdqdt+qC=0
Hint: Use the relationship between current and charge to express the equation in terms of charge.
4. Compare the Two Equations:
Now we have two equations:
- Damped oscillator: md2xdt2+bdxdt+kx=0
- LCR circuit: Ld2qdt2+Rdqdt+qC=0
By comparing coefficients, we can establish the following equivalences:
- m↔L (mass corresponds to inductance)
- b↔R (damping constant corresponds to resistance)
- k↔1C (spring constant corresponds to the reciprocal of capacitance)
Hint: Look for the corresponding terms in both equations to establish equivalences.
5. Establish the Final Equivalences:
From the comparisons, we can summarize:
- Charge q is analogous to displacement x
- Current i is analogous to velocity dxdt
- Voltage V is analogous to force F
Hint: Identify how each physical quantity in the LCR circuit corresponds to the quantities in the damped oscillator.
Conclusion:
The correct equivalences based on the analysis are:
- q↔x
- i↔dxdt
- V↔F
- b↔R
- m↔L
Thus, the correct answer is the first option that matches these equivalences.
The equation for a damped harmonic oscillator (spring-mass system) is given by:
md2xdt2+bdxdt+kx=0
Here, m is the mass, b is the damping constant, k is the spring constant, x is the displacement, and dxdt is the velocity.
For an LCR circuit, applying Kirchhoff's voltage law gives:
Ldidt+Ri+qC=0
where L is the inductance, R is the resistance, C is the capacitance, i is the current, and q is the charge on the capacitor.
The current i is the rate of change of charge q:
i=dqdt
Substitute this into the LCR equation:
Ld2qdt2+Rdqdt+qC=0
Now we have two equations:
- Damped oscillator: md2xdt2+bdxdt+kx=0
- LCR circuit: Ld2qdt2+Rdqdt+qC=0
- m↔L (mass corresponds to inductance)
- b↔R (damping constant corresponds to resistance)
- k↔1C (spring constant corresponds to the reciprocal of capacitance)
From the comparisons, we can summarize:
- Charge q is analogous to displacement x
- Current i is analogous to velocity dxdt
- Voltage V is analogous to force F
The correct equivalences based on the analysis are:
- q↔x
- i↔dxdt
- V↔F
- b↔R
- m↔L
Topper's Solved these Questions
Similar Questions
An LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
View SolutionAn LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
View SolutionA LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q0. then the amplitude of the amount of charge on the capacitor as a function of time t will be:
View SolutionA LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q0. then the amplitude of the amount of charge on the capacitor as a function of time t will be:
View SolutionA LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C□ inductor L having resistance R is oscillatory. Then which of following is correct _____.
View SolutionA LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C□ inductor L having resistance R is oscillatory. Then which of following is correct _____.
View SolutionAn LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
View SolutionThere is a LCR circuit , If it is compared with a damped oscillation of mass m oscillating with force constant k and damping coefficient 'b'. Compare the terms of damped oscillation with the devices in LCR circuit.
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If buoyant force were also taken into account then value of terminal speed would have
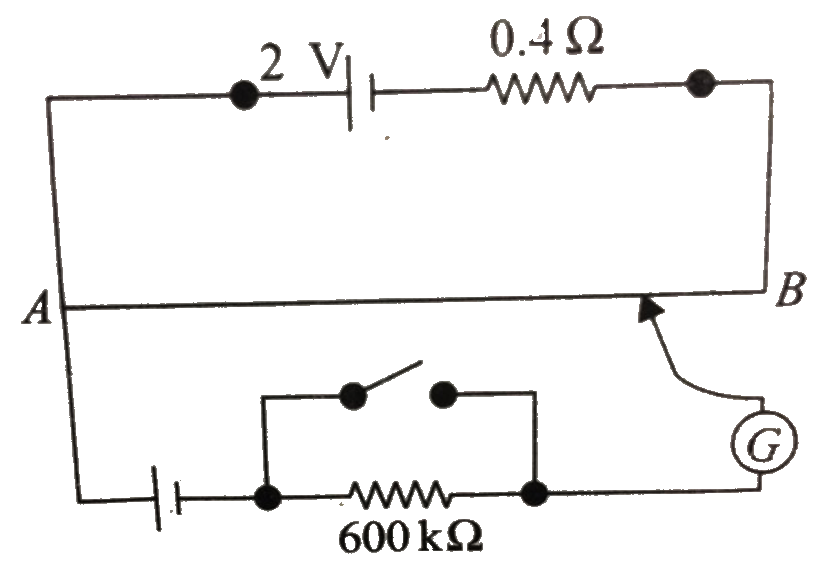
View SolutionFigure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?
View Solution
