The angle of elevation of the top of a vertical tower from a point A due east of it is 45∘. The angle of elevation of the top of the same tower from a point B due south of A is 30∘. If the distance between A and B is 54√2 m then the height of the tower (in metres), is
108
36√3
54√3
54
The correct Answer is:D
To solve the problem step by step, we will use trigonometric principles and the Pythagorean theorem.
Step 1: Understand the Geometry
Let's denote:
- O: the top of the tower
- P: the base of the tower
- A: the point due east of the tower
- B: the point due south of A
From the problem, we know:
- The angle of elevation from A to O is 45∘.
- The angle of elevation from B to O is 30∘.
- The distance between A and B is 54√2 m.
Step 2: Set Up the Triangles
1. In triangle OAP (where A is due east of P):
- Let the height of the tower (OP) be h.
- Let the distance AP (horizontal distance from A to P) be x.
- From the angle of elevation 45∘:
tan(45∘)=hx⟹1=hx⟹h=x
2. In triangle OBP (where B is due south of A):
- Let the distance BP (horizontal distance from B to P) be y.
- From the angle of elevation 30∘:
tan(30∘)=hy⟹1√3=hy⟹y=h√3
Step 3: Relate the Distances
From the geometry, the distance AB can be expressed as:
AB=AP+BP=x+y
Given that AB=54√2, we can substitute y:
x+h√3=54√2
Step 4: Substitute h with x
Since we found that h=x, we can substitute h in the equation:
x+x√3=54√2
Factoring out x:
x(1+√3)=54√2
Now, solve for x:
x=54√21+√3
Step 5: Rationalize the Denominator
To simplify x:
x=54√2(1−√3)(1+√3)(1−√3)=54√2(1−√3)1−3=54√2(1−√3)−2
Thus,
x=−27√2(1−√3)
Step 6: Calculate h
Since h=x, we have:
h=−27√2(1−√3)
Calculating this gives us the height of the tower.
Step 7: Final Calculation
We can also find h directly using the relation:
h2+(54√2)2=(h√3)2
This leads us to:
h2+2916=3h2
Thus,
2h2=2916⟹h2=1458⟹h=√1458=54 m
Final Answer
The height of the tower is 54 meters.
Let's denote:
- O: the top of the tower
- P: the base of the tower
- A: the point due east of the tower
- B: the point due south of A
- The angle of elevation from A to O is 45∘.
- The angle of elevation from B to O is 30∘.
- The distance between A and B is 54√2 m.
1. In triangle OAP (where A is due east of P):
- Let the height of the tower (OP) be h.
- Let the distance AP (horizontal distance from A to P) be x.
- From the angle of elevation 45∘:
tan(45∘)=hx⟹1=hx⟹h=x
- Let the distance BP (horizontal distance from B to P) be y.
- From the angle of elevation 30∘:
tan(30∘)=hy⟹1√3=hy⟹y=h√3
From the geometry, the distance AB can be expressed as:
AB=AP+BP=x+y
Given that AB=54√2, we can substitute y:
x+h√3=54√2
Since we found that h=x, we can substitute h in the equation:
x+x√3=54√2
Factoring out x:
x(1+√3)=54√2
Now, solve for x:
x=54√21+√3
To simplify x:
x=54√2(1−√3)(1+√3)(1−√3)=54√2(1−√3)1−3=54√2(1−√3)−2
Thus,
x=−27√2(1−√3)
Since h=x, we have:
h=−27√2(1−√3)
Calculating this gives us the height of the tower.
We can also find h directly using the relation:
h2+(54√2)2=(h√3)2
This leads us to:
h2+2916=3h2
Thus,
2h2=2916⟹h2=1458⟹h=√1458=54 m
The height of the tower is 54 meters.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLEBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF TRIANGLEEXERCISE - JEE Advanced (Archive)
50 Videos
- PROPERTIES OF TRIANGLEBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF TRIANGLEEXERCISE - Level - 2
55 Videos
- PROBABILITYBOOK - VMC MODULES ENGLISHCHAPTER - PROBABILITYEXERCISE - JEE ADVANCED (ARCHIVE)
102 Videos
- QUADRATIC EQUATIONS & INEQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - QUADRATIC EQUATIONS & INEQUATIONS EXERCISE - JEE Advance ( Archive )
20 Videos
Similar Questions
The angle of elevation of the top of a tower at a point on the ground is 30∘ . What will be the angle of elevation, if the height of the tower is tripled?
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two and also the height of the tower.
View Solution
Knowledge Check
The angle of elevation of the top of a tower. from a point on the ground and at a distance of 160 m from its foot, is find to be 60∘ . Find the height of the tower .
A277.12 mB377.12 mC477.12 mDNone
The angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower a point A due south of it is 30∘ and from a point B due west of it is 45∘ .If the height of the tower is 100 meters ,then find the distance AB.
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also the height of the other tower.
View SolutionThe angle of elevation of the top of a hill at the foot of a tower is 60∘ and the angle of elevation of the top of the tower from the foot of the hill is 30∘ . If the tower is 50 m high, what is the height of the hill?
View Solution
If figure, the angle of elevation of the top of a tower from a point C on the ground which is 30 m away from the foot of the tower, is 30∘. Find th height of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
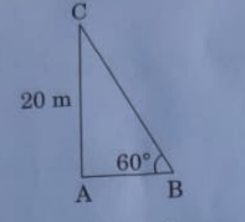
View Solution
