Circles with radii 3,4 and 5 touch each other externally, if P is the point of intersecton of tangents to these circles at their points of contact and the distance of P from the points of contact is √λ, then find the numerical quantity λ.
The correct Answer is:√5
Step by step video solution for Circles with radii 3, 4 and 5 touch each other externally, if P is the point of intersecton of tangents to these circles at their points of contact and the distance of P from the points of contact is sqrt(lambda), then find the numerical quantity lambda. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLEBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF TRIANGLEEXERCISE - JEE Main (Archive)
35 Videos
- PROBABILITYBOOK - VMC MODULES ENGLISHCHAPTER - PROBABILITYEXERCISE - JEE ADVANCED (ARCHIVE)
102 Videos
- QUADRATIC EQUATIONS & INEQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - QUADRATIC EQUATIONS & INEQUATIONS EXERCISE - JEE Advance ( Archive )
20 Videos
Similar Questions
Circles with radii 3, 4 and 5 touch each other externally. If P is the point of intersection of tangents to these circles at their points of contact, then if the distance of P from the points of contact is λ then λ2 is _____
View SolutionCircles of radii 3,4,5 touch each other externally . Let P be the point of intersection of tangents of these circles at their points of contact .Show that the distance of P from a point of contact is √5.
View Solution
Knowledge Check
Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
A32 cmB50 cmC40 cmD30 cm
Three circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is (abca+b+c)12.
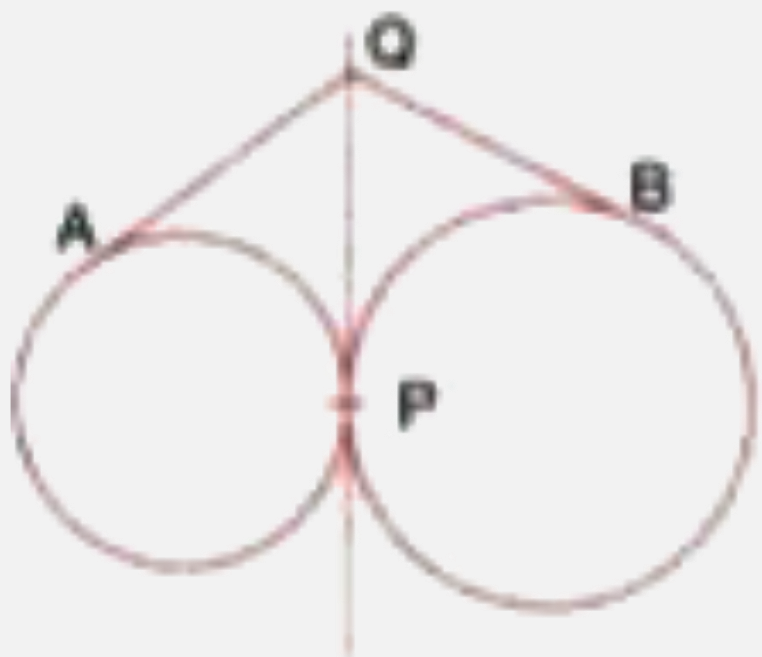
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
View SolutionFind the points of contact Q and R of a tangent from the point P(2,3) on the parabola y2=4x.
View SolutionFind the points of contact Q and R of a tangent from the point P(2,3) on the parabola y2=4x.
View SolutionThree circles touch each other externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 4. Then, the ratio of their product of radii to the sum of the radii is
View SolutionThree circles touch each other externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 4. Then, the ratio of their product of radii to the sum of the radii is
View SolutionThe curve xy=c(c>0) and the circle x2+y2=1 touch at two points, then distance between the points of contact is
View Solution
