The product of all nth root of unity is always
1
−1
1 or –1 depending on n is even or odd
1 or –1 depending on n is odd or even
The correct Answer is:D
To solve the problem of finding the product of all nth roots of unity, we can follow these steps:
1. Understanding nth Roots of Unity:
The nth roots of unity are the solutions to the equation zn=1. These roots can be expressed in the form:
zk=e2πik/nfor k=0,1,2,…,n−1
2. Writing the Product of Roots:
The product of all nth roots of unity can be represented as:
P=z0⋅z1⋅z2⋯zn−1=e2πi⋅0/n⋅e2πi⋅1/n⋅e2πi⋅2/n⋯e2πi⋅(n−1)/n
3. Simplifying the Product:
This product can be simplified using properties of exponents:
P=e2πi(0+1+2+…+(n−1))/n
The sum 0+1+2+…+(n−1) can be calculated using the formula for the sum of the first n−1 integers:
Sum=(n−1)n2
Thus, we have:
P=e2πi⋅(n−1)n/2n=eπi(n−1)
4. Evaluating eπi(n−1):
The expression eπi(n−1) can be evaluated based on whether n−1 is even or odd:
- If n−1 is even (i.e., n is odd), then eπi(n−1)=1.
- If n−1 is odd (i.e., n is even), then eπi(n−1)=−1.
5. Conclusion:
Therefore, the product of all nth roots of unity is:
P=(−1)n−1
This means:
- If n is odd, the product is 1.
- If n is even, the product is −1.
Final Answer:
The product of all nth roots of unity is 1 if n is odd and −1 if n is even.
---
The nth roots of unity are the solutions to the equation zn=1. These roots can be expressed in the form:
zk=e2πik/nfor k=0,1,2,…,n−1
The product of all nth roots of unity can be represented as:
P=z0⋅z1⋅z2⋯zn−1=e2πi⋅0/n⋅e2πi⋅1/n⋅e2πi⋅2/n⋯e2πi⋅(n−1)/n
This product can be simplified using properties of exponents:
P=e2πi(0+1+2+…+(n−1))/n
The sum 0+1+2+…+(n−1) can be calculated using the formula for the sum of the first n−1 integers:
Sum=(n−1)n2
Thus, we have:
P=e2πi⋅(n−1)n/2n=eπi(n−1)
The expression eπi(n−1) can be evaluated based on whether n−1 is even or odd:
- If n−1 is even (i.e., n is odd), then eπi(n−1)=1.
- If n−1 is odd (i.e., n is even), then eπi(n−1)=−1.
Therefore, the product of all nth roots of unity is:
P=(−1)n−1
This means:
- If n is odd, the product is 1.
- If n is even, the product is −1.
The product of all nth roots of unity is 1 if n is odd and −1 if n is even.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - LEVEL - 2
50 Videos
- COMPLEX NUMBERS BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - NUMRICAL VALUE TYPE FOR JEE MAIN
14 Videos
- COMPLEX NUMBERS BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - JEE ARCHIVE
76 Videos
- CIRCLESBOOK - VMC MODULES ENGLISHCHAPTER - CIRCLESEXERCISE - JEE ADVANCED ( ARCHIVE )
68 Videos
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE
76 Videos
Similar Questions
A tap roots is always
View SolutionShow that product of any n consecutive integers is always divisible by n!
View SolutionThe product of the roots of the equation whose roots are greater by unity than the equation x3−5x2+6x−3=0 is equal to
View SolutionThe number of 15th roots of unity which are also the 25th root of unity is: 3 (b) 5 (c) 10 (d) None of these
View SolutionIf z1 and z2 are two of the 8th roots of unity such that arg(z1z2) is last positive, then z1z2 is
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
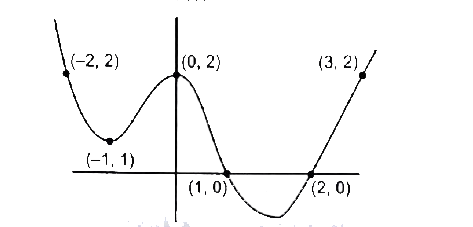
The product of all imaginary roots of p(x)=0 is:
View Solution$ Soil solutIon is absorbed by all the parts of a root .
! Soil solution is always of a high concentration.
View SolutionIf a,b,c are pth,qthandrth term of an AP and GP both, then the product of the roots of equation abbccax2−abcx+acbcca=0 is equal to :
View SolutionIf the arithmetic mean of the product of all pairs of positive integers whose sum is n is An then limn→∞n2An equals to
View SolutionIf α is an nth roots of unity, then 1+2α+3α2+……..+nαn−1 equals
View Solution
