A circle passes through three points A, B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle.If angles DAB and CAB are α and β respectively and the distance between the point A and the mid-point of the line segment DC is d, prove that the area of the circle is πd2cos2acos2α+cos2β+2cosαcosβcos(β−α)
To solve the problem step by step, we will use the information provided in the question and the insights from the video transcript.
Step 1: Understand the Geometry
We have a circle that passes through points A, B, and C, with AC as the diameter. A line through A intersects the chord BC at point D. We know the angles DAB and CAB are denoted as α and β, respectively. The distance from A to the midpoint of segment DC is d.
Step 2: Set Up the Coordinate System
Let’s place the points in a coordinate system:
- Point A at (-r, 0)
- Point C at (r, 0)
- The center of the circle O at (0, 0) with radius r.
Step 3: Define the Points B and D
Let the coordinates of point B be:
- B=(rcos(2β),rsin(2β))
Point D lies on the chord BC. We need to find the coordinates of D based on the angles α and β.
Step 4: Find the Slope of Line AD
The slope of line AD can be expressed using the angle α:
- mAD=tan(α)
Step 5: Write the Equation of Line AD
Using point A and the slope:
- The equation of line AD is:
y−0=tan(α)(x+r)
Rearranging gives:
y=tan(α)(x+r)
Step 6: Find the Equation of Chord BC
The equation of chord BC can be derived using the coordinates of B and C:
- The slope of BC is:
mBC=rsin(2β)−0rcos(2β)−r=sin(2β)cos(2β)−1
- The equation of line BC is:
y−rsin(2β)=mBC(x−rcos(2β))
Step 7: Solve for Intersection Point D
To find point D, we set the equations of lines AD and BC equal to each other and solve for x and y. This will give us the coordinates of D.
Step 8: Find the Midpoint of DC
Let M be the midpoint of segment DC. The coordinates of M can be expressed as:
M=(xD+xC2,yD+yC2)
The distance from A to M is given as d.
Step 9: Relate d to r
Using the distance formula, we can relate d to the radius r and the angles α and β. We will express d in terms of r and the angles.
Step 10: Area of the Circle
The area of the circle is given by:
Area=πr2
Substituting the expression we derived for r in terms of d, α, and β, we arrive at:
Area=πd2cos2(α)cos2(α)+cos2(β)+2cos(α)cos(β)cos(β−α)
Conclusion
We have shown that the area of the circle can be expressed in the required form.
---
We have a circle that passes through points A, B, and C, with AC as the diameter. A line through A intersects the chord BC at point D. We know the angles DAB and CAB are denoted as α and β, respectively. The distance from A to the midpoint of segment DC is d.
Let’s place the points in a coordinate system:
- Point A at (-r, 0)
- Point C at (r, 0)
- The center of the circle O at (0, 0) with radius r.
Let the coordinates of point B be:
- B=(rcos(2β),rsin(2β))
The slope of line AD can be expressed using the angle α:
- mAD=tan(α)
Using point A and the slope:
- The equation of line AD is:
y−0=tan(α)(x+r)
Rearranging gives:
y=tan(α)(x+r)
The equation of chord BC can be derived using the coordinates of B and C:
- The slope of BC is:
mBC=rsin(2β)−0rcos(2β)−r=sin(2β)cos(2β)−1
- The equation of line BC is:
y−rsin(2β)=mBC(x−rcos(2β))
To find point D, we set the equations of lines AD and BC equal to each other and solve for x and y. This will give us the coordinates of D.
Let M be the midpoint of segment DC. The coordinates of M can be expressed as:
M=(xD+xC2,yD+yC2)
The distance from A to M is given as d.
Using the distance formula, we can relate d to the radius r and the angles α and β. We will express d in terms of r and the angles.
The area of the circle is given by:
Area=πr2
Substituting the expression we derived for r in terms of d, α, and β, we arrive at:
Area=πd2cos2(α)cos2(α)+cos2(β)+2cos(α)cos(β)cos(β−α)
We have shown that the area of the circle can be expressed in the required form.
Topper's Solved these Questions
Similar Questions
If a number of circles pass through the end points P and Q of a line segment PQ, then prove their centres lie on the perpendicular bisector of PQ.
View SolutionGiven points A(1,5),B(−3,7)andC(15,9)
Find the equation of a line passing through the mid-point of AC and the point B.
View SolutionFind the slope of the line which passes through the origin and the mid-point of the line segment joining the points A(0,−4)andB(8,0).
View SolutionIf a number of circles pass through the end points P and Q of a line segment PQ, then Prove that their centres lie on the perpendicular bisector of PQ.
View SolutionThe slope of a line which passes through the origin the mid-point of the line segment joining the points (0,−4) and (8,0) is
View SolutionFind the equation of a line perpendicular to the line xa+yb−1 and passes through the mid-point of the line segment lying between the axes of the given line.
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionIf two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
View SolutionA circle passing through the vertex C of a rectangle ABCD and touching its sides AB and AD at M and N, respectively. If the distance from C to the line segment MN is equal to 5 units, then find the area of the reactangle ABCD.
View Solution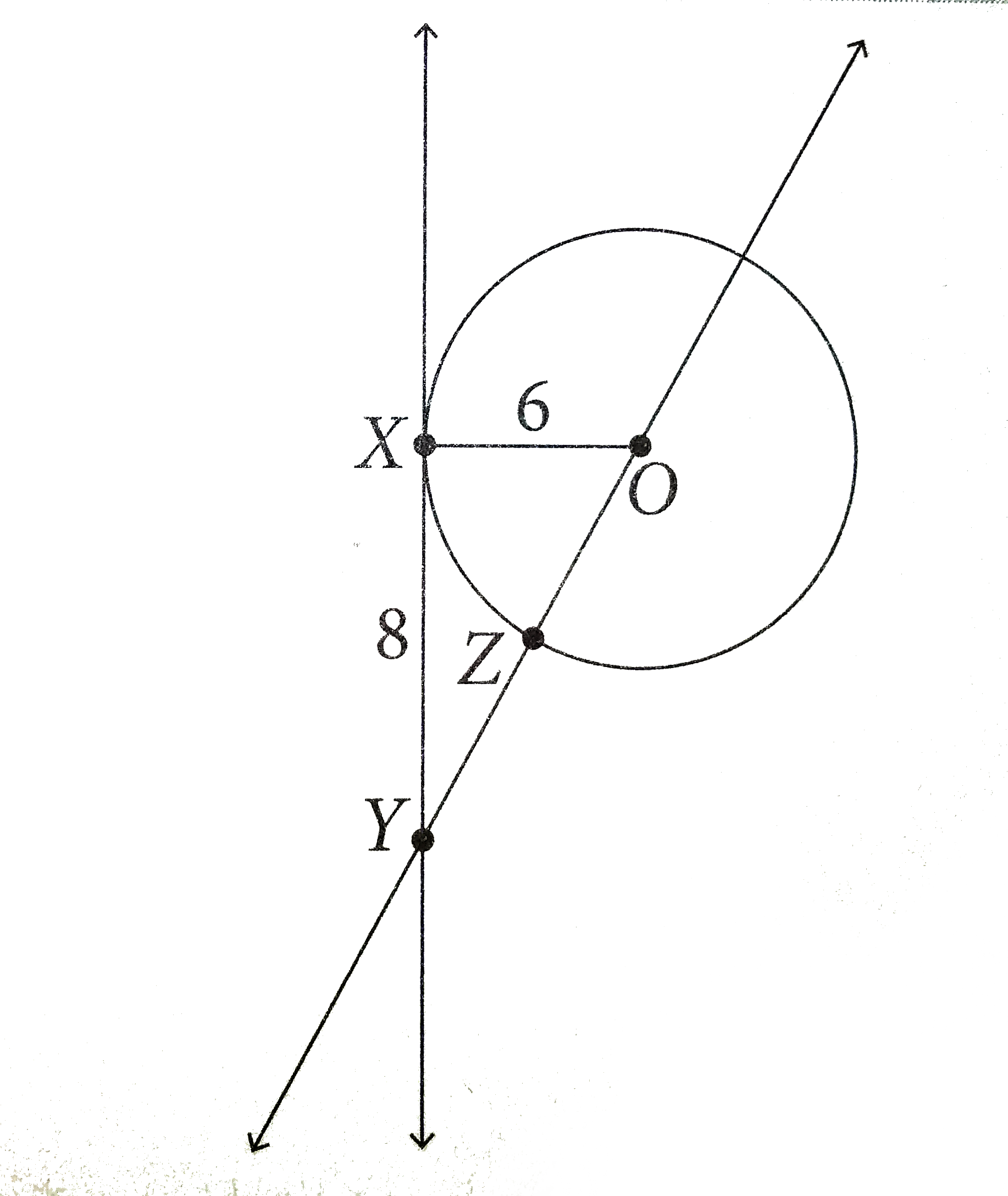
In the figure above, O is the center of the circle, the length of segment XY is 8, and the line passing through point X and Y is tangent to the circle at point X. What is the length of segment ZY?
View Solution
