A circle passing through the vertex C of a rectangle ABCD and touching its sides AB and AD at M and N, respectively. If the distance from C to the line segment MN is equal to 5 units, then find the area of the reactangle ABCD.
To solve the problem, we need to find the area of rectangle ABCD given that a circle passes through vertex C and touches sides AB and AD at points M and N, respectively. The distance from point C to line segment MN is given as 5 units.
1. Understanding the Geometry:
- Draw rectangle ABCD with vertices A, B, C, and D.
- The circle touches side AB at point M and side AD at point N.
- The distance from point C to line segment MN is given as 5 units.
2. Identify the Tangents:
- Since the circle touches the sides AB and AD, we know that line segments AM and AN are tangents to the circle at points M and N, respectively.
3. Use of the Alternate Segment Theorem:
- By the alternate segment theorem (or tangent-secant theorem), the angles formed by the tangents and the chords are equal.
- This means that angles ∠MCA and ∠NCD are equal to the angles formed by the tangents at points M and N.
4. Establishing Right Angles:
- The distance from point C to line segment MN is the shortest distance, which is perpendicular to MN. Thus, we can denote this distance as a right angle (90 degrees).
5. Triangles Involved:
- Consider triangles CND and CMB.
- Since we have established that these triangles share angles and have right angles, we can use the properties of similar triangles.
6. Setting Up Proportions:
- From the similarity of triangles, we can set up the following ratios:
CNCM=CDCE
- Similarly, for triangles CMB and CEN:
CBCE=CMCN
7. Cross Multiplying:
- From the above ratios, we can cross-multiply to find relationships between the segments:
CN⋅CE=CM⋅CD
8. Using the Given Distance:
- We know that the distance from C to MN is 5 units, which can be used to express the lengths of segments in terms of the rectangle's dimensions.
9. Finding the Area:
- The area of rectangle ABCD is given by the product of its sides, which can be expressed as:
Area=CB⋅CD
- From the relationships established, we find that:
CB⋅CD=25
- Thus, the area of rectangle ABCD is 25 square units.
Final Result:
The area of rectangle ABCD is 25 square units.
---
- Draw rectangle ABCD with vertices A, B, C, and D.
- The circle touches side AB at point M and side AD at point N.
- The distance from point C to line segment MN is given as 5 units.
- Since the circle touches the sides AB and AD, we know that line segments AM and AN are tangents to the circle at points M and N, respectively.
- By the alternate segment theorem (or tangent-secant theorem), the angles formed by the tangents and the chords are equal.
- This means that angles ∠MCA and ∠NCD are equal to the angles formed by the tangents at points M and N.
- The distance from point C to line segment MN is the shortest distance, which is perpendicular to MN. Thus, we can denote this distance as a right angle (90 degrees).
- Consider triangles CND and CMB.
- Since we have established that these triangles share angles and have right angles, we can use the properties of similar triangles.
- From the similarity of triangles, we can set up the following ratios:
CNCM=CDCE
- Similarly, for triangles CMB and CEN:
CBCE=CMCN
- From the above ratios, we can cross-multiply to find relationships between the segments:
CN⋅CE=CM⋅CD
- We know that the distance from C to MN is 5 units, which can be used to express the lengths of segments in terms of the rectangle's dimensions.
- The area of rectangle ABCD is given by the product of its sides, which can be expressed as:
Area=CB⋅CD
- From the relationships established, we find that:
CB⋅CD=25
- Thus, the area of rectangle ABCD is 25 square units.
The area of rectangle ABCD is 25 square units.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Examples13videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
ABCD is a rectangle. A circle passing through vertex C touches the sides AB and AD at M and N respectively. If the distance lof the line MN from the vertex C is P units then the area of rectangle ABCD is
View SolutionletABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, ABCD is a rectangle and E is a point on the side AB. If AB=10andAD=5 what is the area of the shaded region in the figure?
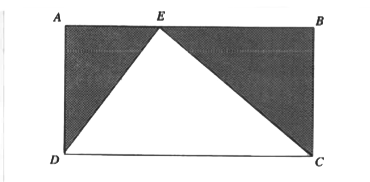 A25B30C35D40
A25B30C35D40
letABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View SolutionA circle passes through three points A, B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle.If angles DAB and CAB are α and β respectively and the distance between the point A and the mid-point of the line segment DC is d, prove that the area of the circle is πd2cos2acos2α+cos2β+2cosαcosβcos(β−α)
View SolutionLet ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
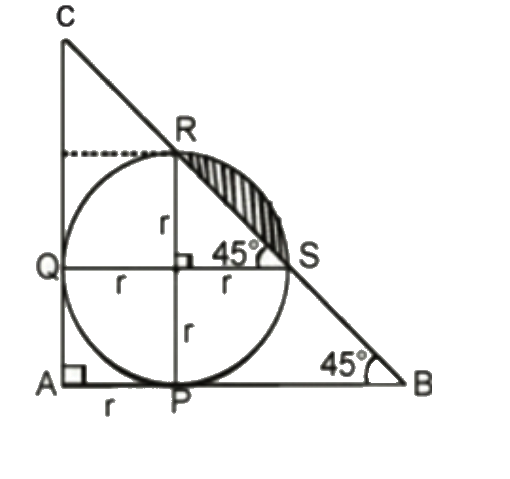
View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
 View Solution
View SolutionThe slope of a median, drawn from the vertex A of the triangle ABC is -2. The co-ordinates of vertices B and C are respectively (-1, 3) and (3, 5). If the area of the triangle be 5 square units, then possible distance of vertex A from the origin is/are.
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionIn Fig. 2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB=29 cm, AD-23 cm,∠B=90° and DS = 5 cm, then the radius of the circle (in cm)
View Solution

