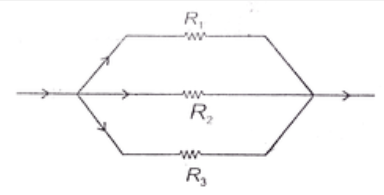
The possible error in computing the parallel resistance R of three resistances from the formula , if are each in error by plus 1.2% is :
0.012
0.013
0.014
0.015
The correct Answer is:A
To find the possible error in computing the parallel resistance R of three resistances R1,R2,R3 given that each resistance has an error of +1.2%, we will follow these steps:
Step 1: Write the formula for parallel resistance
The formula for the total resistance R in parallel is given by:
1R=1R1+1R2+1R3
Step 2: Differentiate the equation
To find the possible error, we differentiate the equation with respect to R:
d(1R)=d(1R1)+d(1R2)+d(1R3)
Using the chain rule, we have:
−dRR2=−dR1R21−dR2R22−dR3R23
Step 3: Rearranging the equation
Rearranging gives us:
dRR=dR1R1+dR2R2+dR3R3
Step 4: Expressing errors as percentages
Given that the errors in R1,R2,R3 are +1.2%, we can express this as:
dR1R1×100=1.2,dR2R2×100=1.2,dR3R3×100=1.2
Thus, we have:
dR1R1=0.012,dR2R2=0.012,dR3R3=0.012
Step 5: Substitute the errors into the equation
Substituting these values into our rearranged equation:
dRR=0.012+0.012+0.012=0.036
Step 6: Calculate the percentage error in R
To find the percentage error in R:
dRR×100=0.036×100=3.6%
Conclusion
The possible error in computing the parallel resistance R is 3.6%.
---
The formula for the total resistance R in parallel is given by:
1R=1R1+1R2+1R3
To find the possible error, we differentiate the equation with respect to R:
d(1R)=d(1R1)+d(1R2)+d(1R3)
Using the chain rule, we have:
−dRR2=−dR1R21−dR2R22−dR3R23
Rearranging gives us:
dRR=dR1R1+dR2R2+dR3R3
Given that the errors in R1,R2,R3 are +1.2%, we can express this as:
dR1R1×100=1.2,dR2R2×100=1.2,dR3R3×100=1.2
Thus, we have:
dR1R1=0.012,dR2R2=0.012,dR3R3=0.012
Substituting these values into our rearranged equation:
dRR=0.012+0.012+0.012=0.036
To find the percentage error in R:
dRR×100=0.036×100=3.6%
The possible error in computing the parallel resistance R is 3.6%.
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - Level -2
69 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - Numerical ValueType for JEE Main
14 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)
81 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
- DIFFERENTIAL EQUATIONSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )
32 Videos
Similar Questions
Knowledge Check
When resistors R1andR2 are connected in a parallel electric circuit, the total resistance is 11R1+1R2. This fraction is equivalent to
AR1+R2BR1+R2R1R2CR1R2+R2R1DR1R2R1+R2
prove that : triangle ABC, 1r1+1r2+1r3=1r
View SolutionProve that : 1r1+1r2+1r3=1r
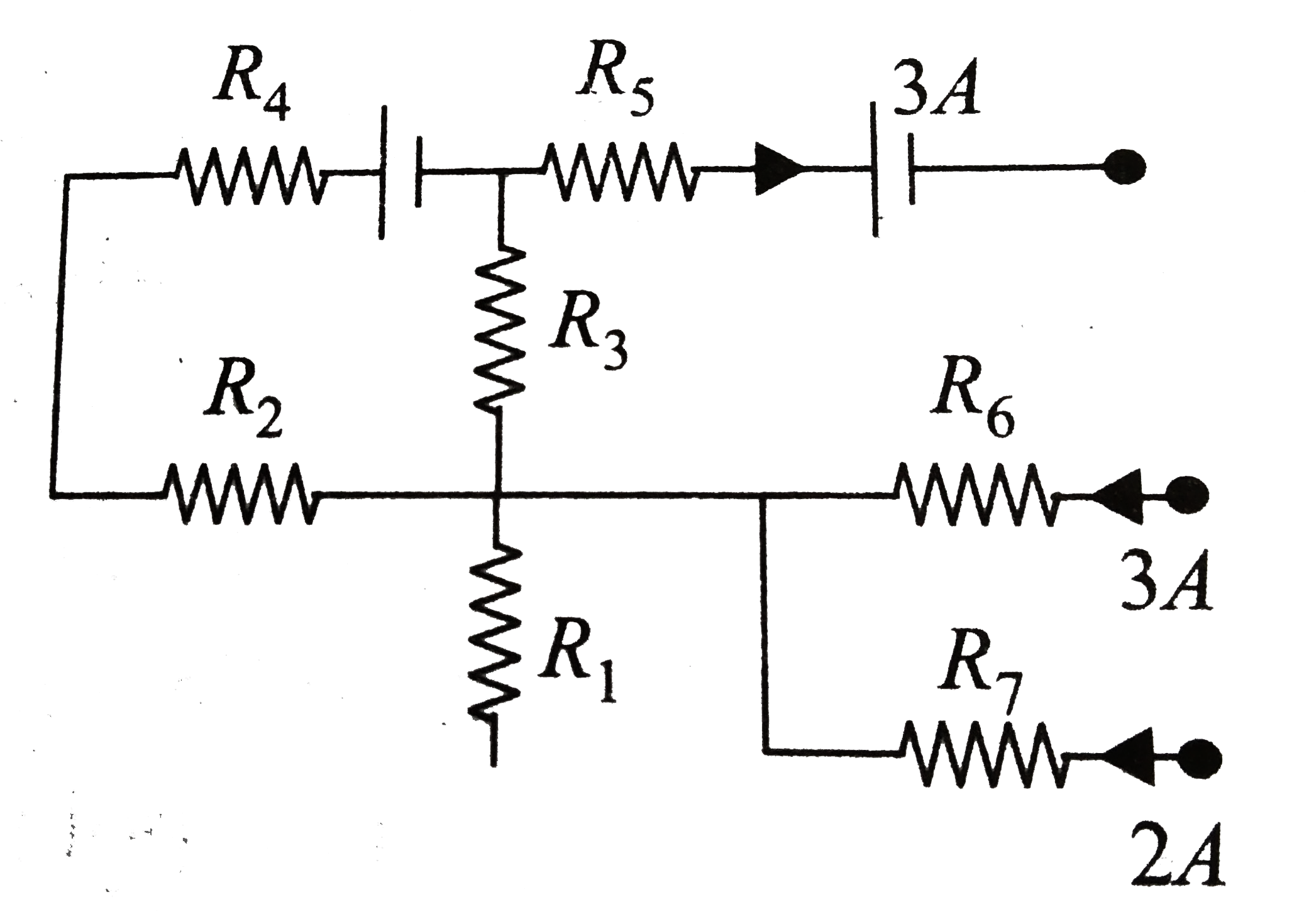
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
 .
.
View SolutionCalculate equivalent resistance of two resistors R1andR2 in parallel where, R1=(6±0.2)ohm and R2=(3±0.1)ohm
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View Solution