Write the expressions for the equivalent resistance R of three resistors R1,R2,andR3 joined in (a) parallel, and (b) series.
To find the equivalent resistance R of three resistors R1,R2, and R3 joined in both parallel and series configurations, we can follow these steps:
(a) Equivalent Resistance in Parallel
1. Understanding Parallel Connection: In a parallel connection, the voltage across each resistor is the same, and the total current is the sum of the currents through each resistor.
2. Using Ohm's Law: According to Ohm's Law, the current through each resistor can be expressed as:
I1=VR1,I2=VR2,I3=VR3
where V is the voltage across the resistors.
3. Total Current: The total current I flowing through the circuit is:
I=I1+I2+I3=VR1+VR2+VR3
4. Factoring Out Voltage: We can factor out V:
I=V(1R1+1R2+1R3)
5. Using Equivalent Resistance: The equivalent resistance R can be defined as:
I=VR
6. Setting the Equations Equal: By equating the two expressions for current, we have:
VR=V(1R1+1R2+1R3)
7. Canceling Voltage: Since V is non-zero, we can cancel it:
1R=1R1+1R2+1R3
8. Finding Equivalent Resistance: Thus, the expression for the equivalent resistance R is:
R=1(1R1+1R2+1R3)
(b) Equivalent Resistance in Series
1. Understanding Series Connection: In a series connection, the same current flows through each resistor, and the total voltage is the sum of the voltages across each resistor.
2. Using Ohm's Law: The voltage across each resistor can be expressed as:
V1=I⋅R1,V2=I⋅R2,V3=I⋅R3
3. Total Voltage: The total voltage V across the series circuit is:
V=V1+V2+V3=I⋅R1+I⋅R2+I⋅R3
4. Factoring Out Current: We can factor out I:
V=I(R1+R2+R3)
5. Using Equivalent Resistance: The equivalent resistance R can also be defined as:
V=I⋅R
6. Setting the Equations Equal: By equating the two expressions for voltage, we have:
I⋅R=I(R1+R2+R3)
7. Canceling Current: Since I is non-zero, we can cancel it:
R=R1+R2+R3
Final Expressions
- For resistors in parallel:
1R=1R1+1R2+1R3
- For resistors in series:
R=R1+R2+R3
I1=VR1,I2=VR2,I3=VR3
where V is the voltage across the resistors.
I=I1+I2+I3=VR1+VR2+VR3
I=V(1R1+1R2+1R3)
I=VR
VR=V(1R1+1R2+1R3)
1R=1R1+1R2+1R3
R=1(1R1+1R2+1R3)
V1=I⋅R1,V2=I⋅R2,V3=I⋅R3
V=V1+V2+V3=I⋅R1+I⋅R2+I⋅R3
V=I(R1+R2+R3)
V=I⋅R
I⋅R=I(R1+R2+R3)
R=R1+R2+R3
1R=1R1+1R2+1R3
R=R1+R2+R3
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (NUMERICALS )
54 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A)(NUMERICALS )
16 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
For the series combination of three resistors establish the relation :
R=R1+R2+R3
where the symbols have their usual meanings.
Calculate the equivalent resistance of the combination of three resistors of 6Ω,9Ω and 18Ω joined in parallel.
View SolutionCalculate equivalent resistance of two resistors R1andR2 in parallel where, R1=(6±0.2)ohm and R2=(3±0.1)ohm
View Solution(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.
View SolutionFind the currents going through the three resistors R1,R2 and R3 in the circuit of figure.

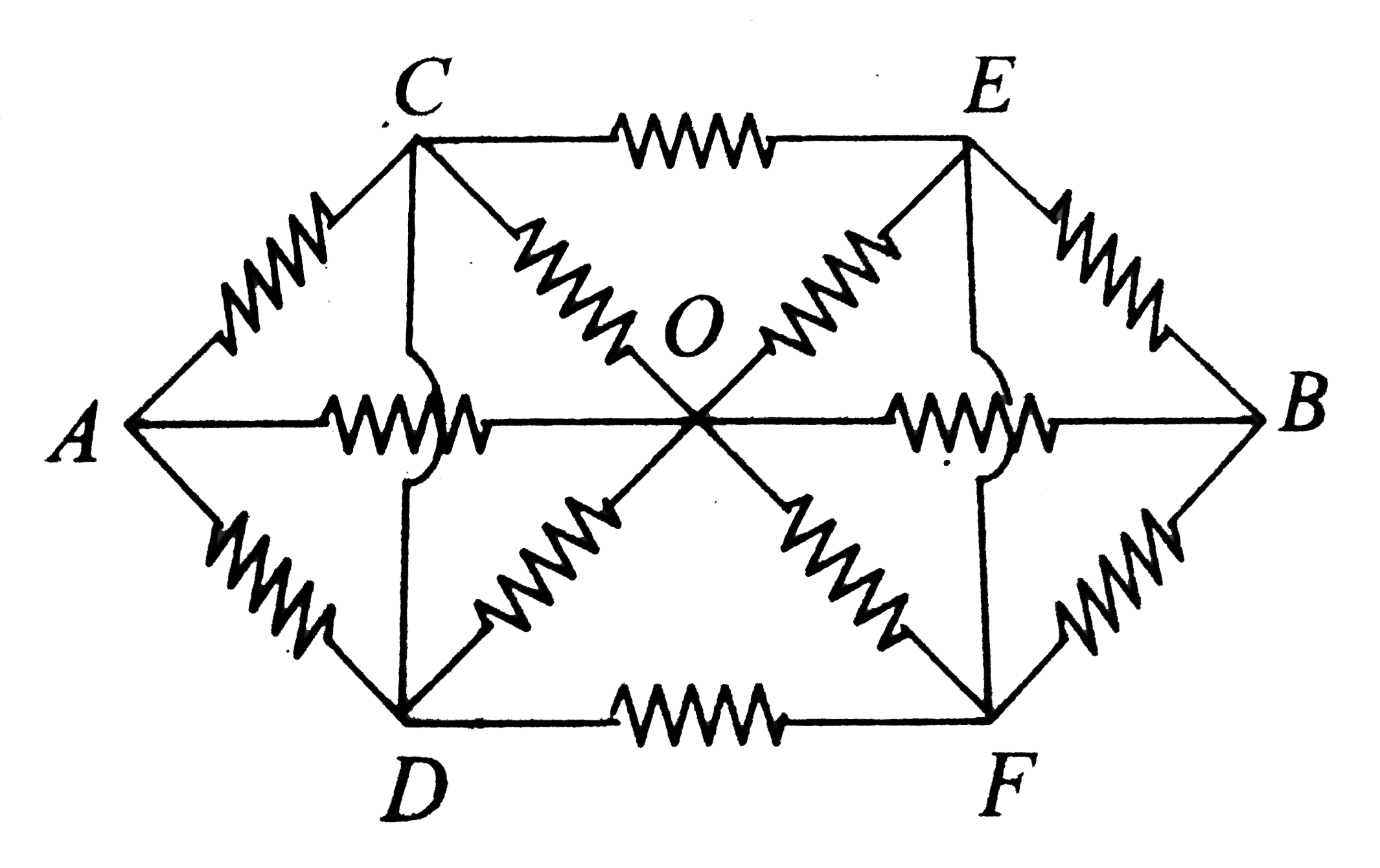
View SolutionFind the equivalent resistance between A and B. Each resistor has same resistance R.
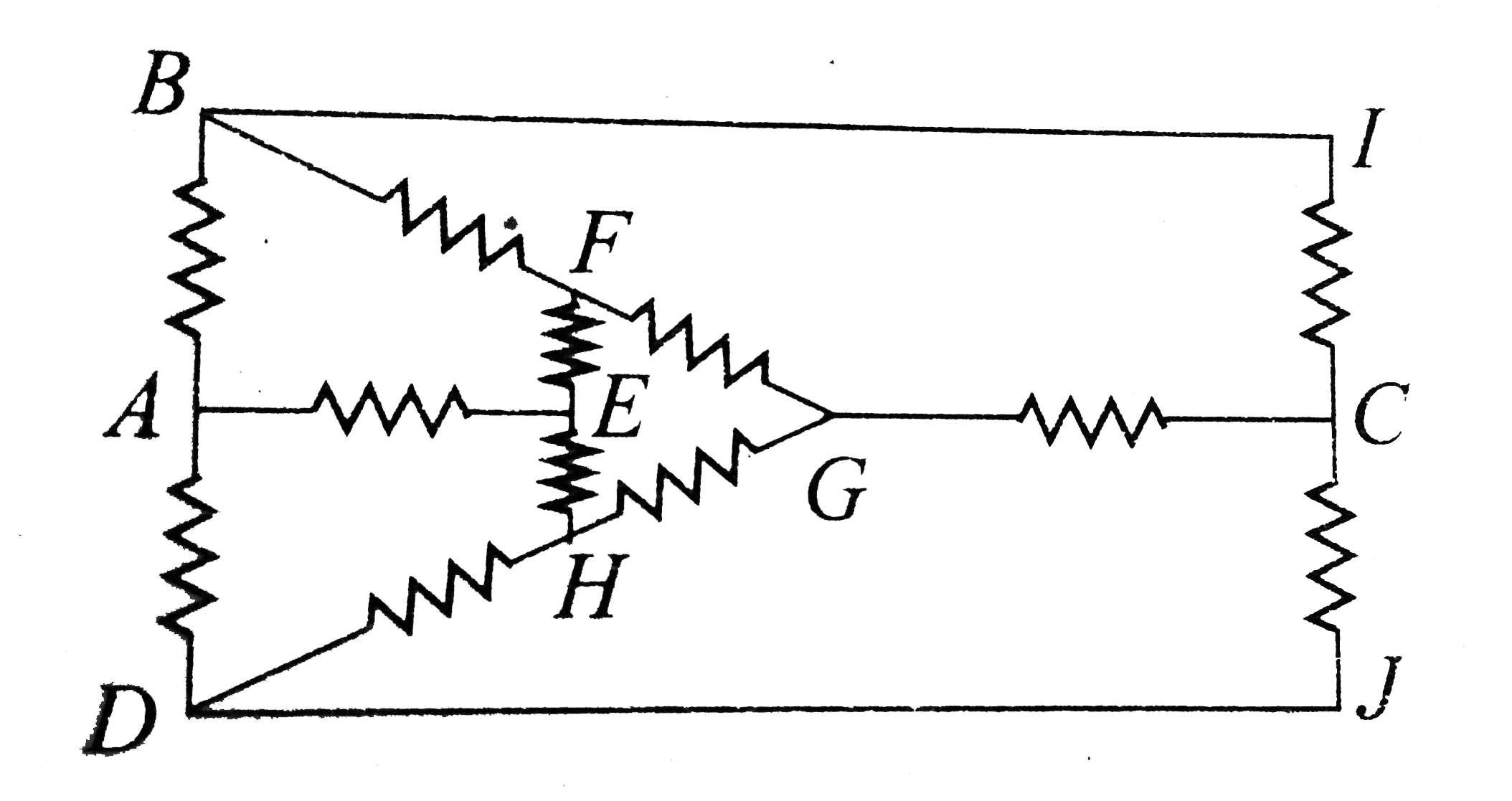
View Solutionfind the equivalent resistance between A and E(resistance of each resistor is R.
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R1+R2 and for (b) 1R'=1R1+1R2 and ΔR'R'2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View Solution
