Let for every real number Then (a) is increasing whenever is increasing (b) is increasing whenever is decreasing (c) is decreasing whenever is decreasing (d) nothing can be said in general
h is increasing, whenever f is increasing
h is increasing, whenever f is decreasing
h is decreasing, whenever f is decreasing
Nothing can be said in general
The correct Answer is:A, C
Step by step video & image solution for Let h(x)=f(x)-(f(x))^2+(f(x))^3 for every real number xdot Then (a) h is increasing whenever f is increasing (b)h is increasing whenever f is decreasing (c)h is decreasing whenever f is decreasing (d) nothing can be said in general by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Main (Archive)
36 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
- DIFFERENTIAL EQUATIONSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )
32 Videos
Similar Questions
Let g(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R. Then prove that g is increasing whenever is increasing.
View SolutionLet g(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R. Then prove that g is increasing whenever is increasing.
View SolutionLet h(x)=f(x)−a(f(x))3 for every real number x
h(x) increase as f(x) increses for all real values of x if
View SolutionThe function f(x)=x1+|x| is (a) strictly increasing (b) strictly decreasing (c) neither increasing nor decreasing (d) none of these
View SolutionThe function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
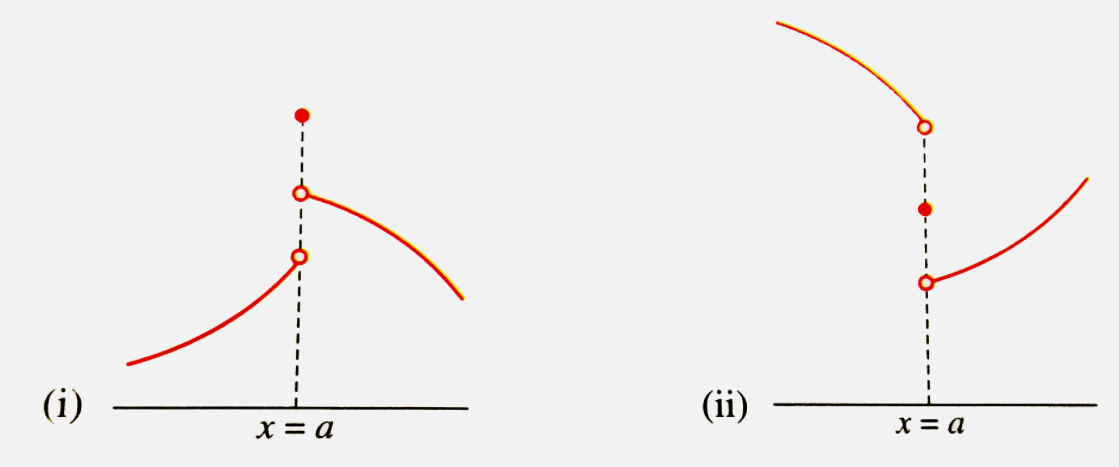
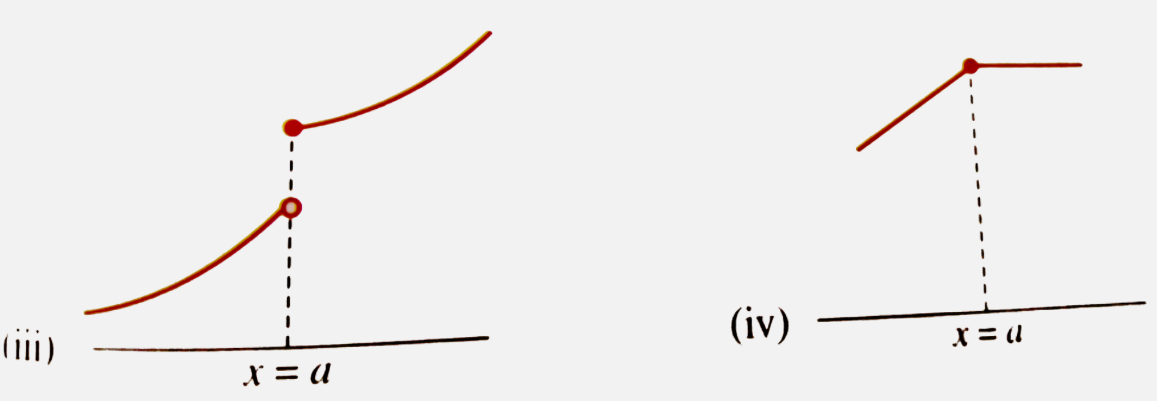
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing.
View SolutionWhich of the following statement is always true? (a)If f(x) is increasing, the f−1(x) is decreasing. (b)If f(x) is increasing, then 1f(x) is also increasing. (c)If fandg are positive functions and f is increasing and g is decreasing, then fg is a decreasing function. (d)If fandg are positive functions and f is decreasing and g is increasing, the fg is a decreasing function.
View SolutionState whether f(x)=tanx−x is increasing or decreasing its domain.
View Solution
