Question

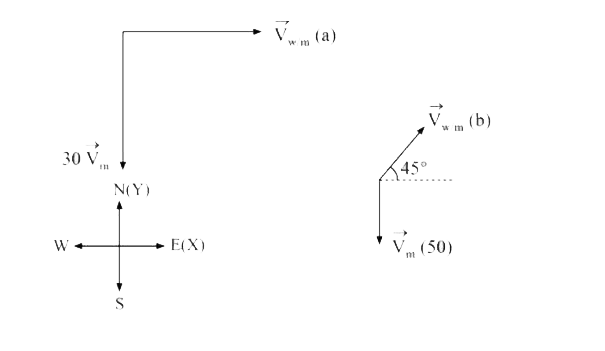
If particles A and B are moving with velocities ${\overrightarrow{V}}_A$ and ${\overrightarrow{V}}_B$ , respectively. The relative velocity of A with respect to B is defined as ${\overrightarrow{V}}_{AB}={\overrightarrow{V}}_{AB}={\overrightarrow{V}}_A-{\overrightarrow{V}}_B$ .



The driver of a car travelling Southward at $30km{h}^{-1}$ observes that wind appears to be coming from the West. The driver of another car travelling Southward at $50km{h}^{-1}$ observes that wind appears to be coming from the South-West.

Options

A. Wind is blowing in a direction `tan^(-1)(3/2)` South to East
B. Wind is blowing in a direction `tan^(-1)(3/2)` North to West
C. The speed of wind is `5sqrt(3) km h^(-1)`
D. The speed of wind is `10sqrt(13) km h^(-1)`

Answer

ad

Explanation

To solve the problem, we need to analyze the situation described in the question step by step, focusing on the velocities of the cars and the apparent wind direction as perceived by the drivers.

Step 1: Understand the scenario
- We have two cars moving southward:
- Car A at a speed of 30 km/h
- Car B at a speed of 50 km/h
- The driver of Car A perceives the wind coming from the west.
- The driver of Car B perceives the wind coming from the southwest.

Step 2: Set up the coordinate system
- Let's define our coordinate system:
- North is in the positive y-direction.
- South is in the negative y-direction.
- East is in the positive x-direction.
- West is in the negative x-direction.

Step 3: Analyze the velocity of the wind with respect to the cars
- The relative velocity of the wind with respect to each car can be defined as:
- For Car A:
\( \overset{\rarr}{V_{wA}} = \overset{\rarr}{V_w} - \overset{\rarr}{V_A} \)
- For Car B:
\( \overset{\rarr}{V_{wB}} = \overset{\rarr}{V_w} - \overset{\rarr}{V_B} \)

Step 4: Determine the wind direction for Car A
- Since Car A observes the wind coming from the west, we can represent this as:
- The wind's apparent velocity vector relative to Car A is directed towards the east (0°).
- This means:
\( \overset{\rarr}{V_{wA}} = \overset{\rarr}{V_w} - (0, -30) \)
- Thus, the wind's velocity vector can be expressed as:
\( \overset{\rarr}{V_w} = (V_{wx}, V_{wy}) \quad \text{and} \quad \overset{\rarr}{V_{wA}} = (V_{wx}, V_{wy} + 30) \)

Step 5: Determine the wind direction for Car B
- Car B perceives the wind coming from the southwest, which is at a 45° angle to the south.
- The apparent wind direction can be represented as:
\( \overset{\rarr}{V_{wB}} = \overset{\rarr}{V_w} - (0, -50) \)
- This means:
\( \overset{\rarr}{V_{wB}} = (V_{wx}, V_{wy} + 50) \)

Step 6: Set up equations based on the apparent wind directions
- For Car A (wind from the west):
\( V_{wy} + 30 = 0 \implies V_{wy} = -30 \)
- For Car B (wind from the southwest):
\( V_{wy} + 50 = -V_{wx} \quad \text{(since wind is at 45°)} \)

Step 7: Solve the equations
- Substitute \( V_{wy} = -30 \) into the equation for Car B:
\( -30 + 50 = -V_{wx} \implies 20 = -V_{wx} \implies V_{wx} = -20 \)

Step 8: Calculate the magnitude of wind velocity
- The wind velocity vector is:
\( \overset{\rarr}{V_w} = (-20, -30) \)
- The magnitude of the wind velocity can be calculated using the Pythagorean theorem:
\( |V_w| = \sqrt{(-20)^2 + (-30)^2} = \sqrt{400 + 900} = \sqrt{1300} = 10\sqrt{13} \text{ km/h} \)

Step 9: Determine the direction of the wind
- The angle \( \theta \) with respect to the east can be calculated using:
\( \tan \theta = \frac{V_{wy}}{V_{wx}} = \frac{-30}{-20} = \frac{3}{2} \)
- Thus, \( \theta = \tan^{-1}(1.5) \).

Final Result
- The wind velocity is \( 10\sqrt{13} \) km/h directed from the east at an angle \( \theta \) south of east.