Range of a projectile with time of flight 10 s and maximum height 100 m is : (g=−10m/s2)
200 m
125 m
100 m
Data incoorect
The correct Answer is:D
To solve the problem of finding the range of a projectile given the time of flight and maximum height, we can follow these steps:
Step 1: Understand the formulas
We have two key formulas for projectile motion:
1. Time of Flight (T): T=2usinθg
2. Maximum Height (H): H=u2sin2θ2g
Where:
- u = initial velocity
- θ = angle of projection
- g = acceleration due to gravity (given as −10m/s2)
Step 2: Use the Time of Flight
Given that the time of flight T=10s, we can set up the equation:
10=2usinθ10
Rearranging gives:
usinθ=50(Equation 1)
Step 3: Use the Maximum Height
Given that the maximum height H=100m, we can set up the equation:
100=u2sin2θ2×10
This simplifies to:
100=u2sin2θ20
Rearranging gives:
u2sin2θ=2000(Equation 2)
Step 4: Substitute Equation 1 into Equation 2
From Equation 1, we have usinθ=50. Squaring both sides gives:
u2sin2θ=2500(Equation 3)
Step 5: Compare Equations 2 and 3
Now we have:
- From Equation 2: u2sin2θ=2000
- From Equation 3: u2sin2θ=2500
Since both equations cannot be true simultaneously, we conclude that the data provided in the problem is inconsistent.
Conclusion
Thus, the range cannot be determined from the given data, and the correct conclusion is that the data is incorrect.
We have two key formulas for projectile motion:
1. Time of Flight (T): T=2usinθg
2. Maximum Height (H): H=u2sin2θ2g
- u = initial velocity
- θ = angle of projection
- g = acceleration due to gravity (given as −10m/s2)
Given that the time of flight T=10s, we can set up the equation:
10=2usinθ10
Rearranging gives:
usinθ=50(Equation 1)
Given that the maximum height H=100m, we can set up the equation:
100=u2sin2θ2×10
This simplifies to:
100=u2sin2θ20
Rearranging gives:
u2sin2θ=2000(Equation 2)
From Equation 1, we have usinθ=50. Squaring both sides gives:
u2sin2θ=2500(Equation 3)
Now we have:
- From Equation 2: u2sin2θ=2000
- From Equation 3: u2sin2θ=2500
Thus, the range cannot be determined from the given data, and the correct conclusion is that the data is incorrect.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A projectile is projected from ground with an initial velocity (5ˆi+10ˆj)m/s If the range of projectile is R m, time of flight is Ts and maximum height attained above ground is Hm, find the numerical value of R×HT. [Take g=10m/s2]
View SolutionAssertion In projectile motion, if time of flight is 4s, then maximum height will be 20 m. (Take, g=10ms−2)
Reason Maximum height =gT2.
View SolutionThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [g=10m/s2]
View SolutionThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [g=10m/s2]
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA body projected with velocity 30 ms−1 reaches its maximum height in 1.5 s. Its range is (g=10ms−2)
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
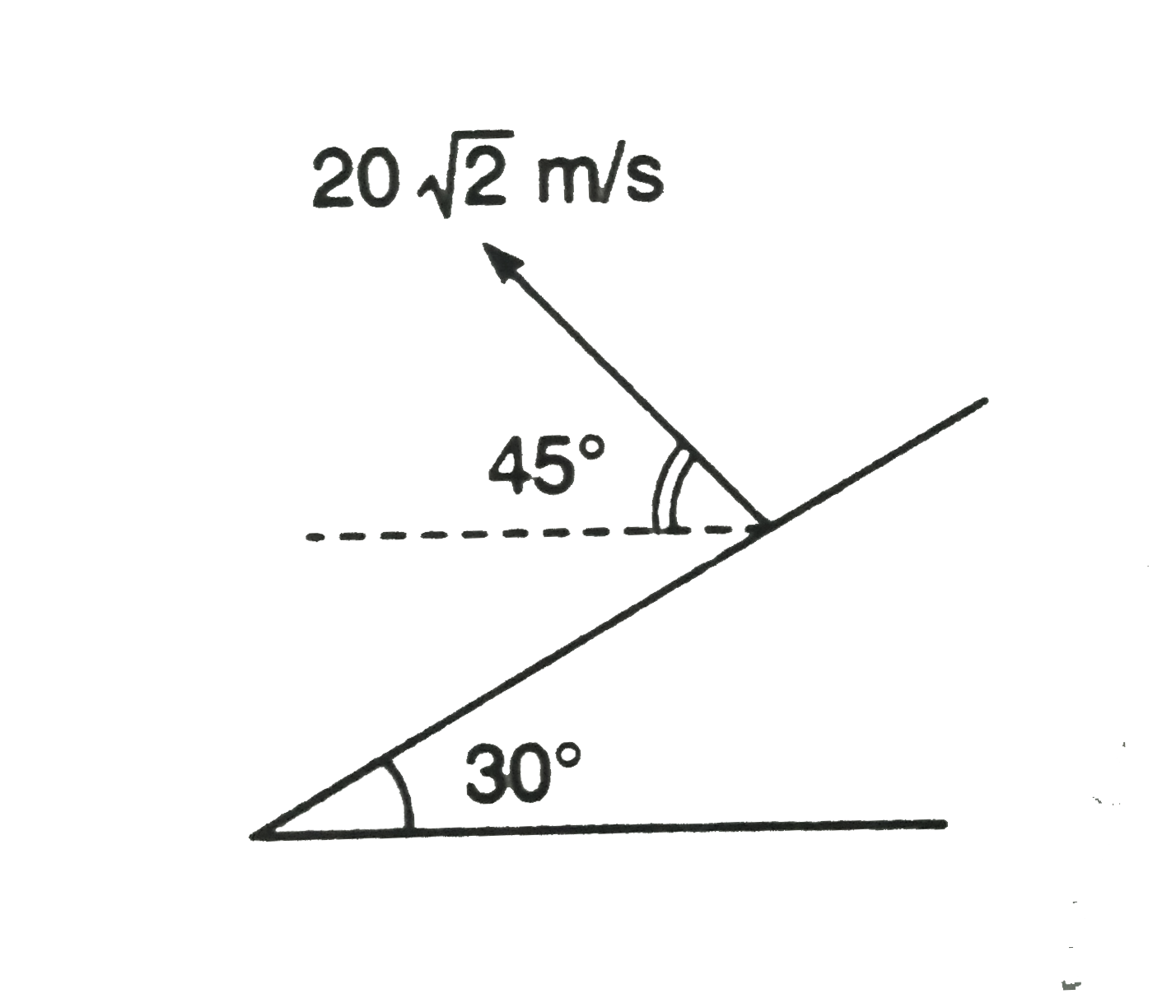
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)

View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
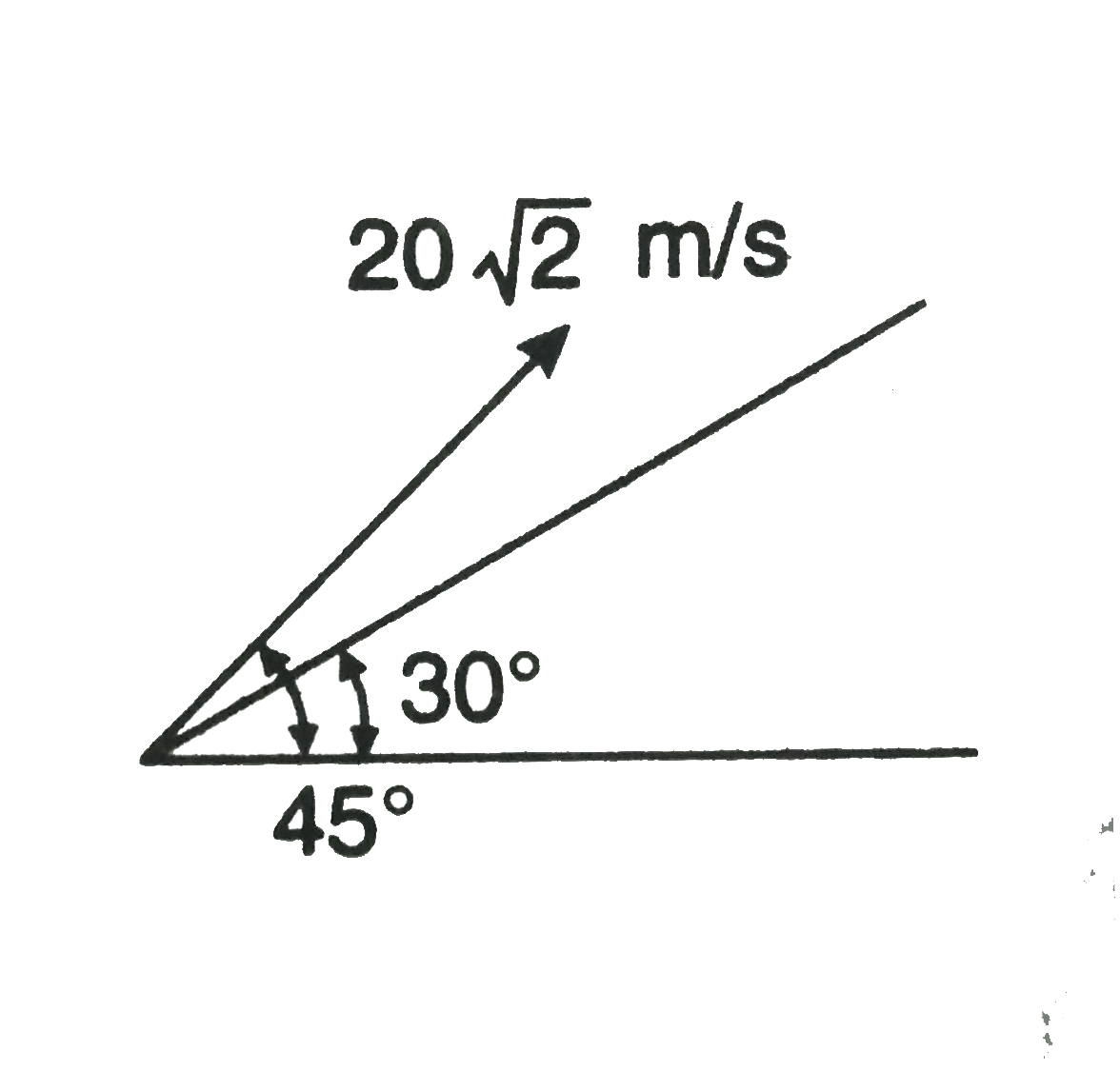
View Solution