Two particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
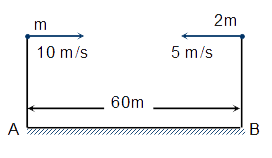
(a)40 m
(b)20 m
(c)30 m
(d)zero
The correct Answer is:A
They will fall through the same height say h. Let them collide at a distance x from tower A.
Solving (ii) and (iii) we get x=20m, t=4 sec, h=89m
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
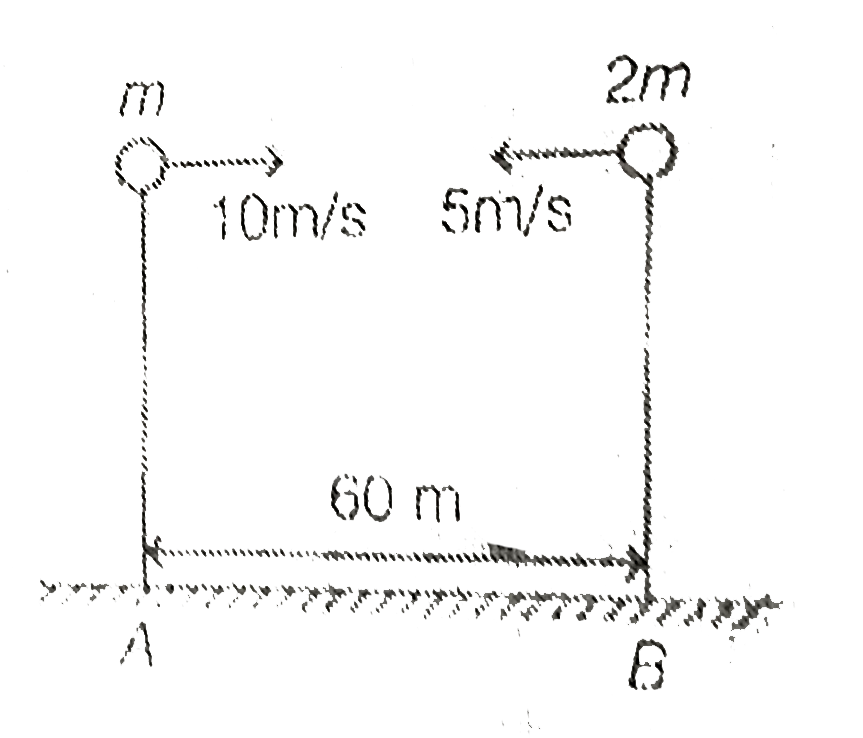
Two particles one of mass m and the other of mass 2 m are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s respectively . They collide in air and stick to each other . The distance from A , where the combined mass finally land is
View SolutionTwo balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is
View SolutionTwo particles A and B of masses 1kg and 2kg respectively are projected in the directions shown in figure with speeds uA=200m/s and uB=50m/s. Initially they were 90m apart. They collide in mid air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant.
(g=10m/s2)

View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionTwo bodies of masses m and 2m are moving along positive x and y axes respectively with equal speed 4ms−1. They collide at origin and stick together. The final velocity of combined mass is
View SolutionTwo towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Find the distance from B where the objects hit the ground.
View SolutionTwo towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Calculate the distance d between the towers.
View SolutionTwo particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View SolutionTwo particles are intially at a separation of d to each other. They move with constant velocirties with 5m/s and 3m/s respectively in horizontal plane. Their velocities makes an angle 60∘ with each other. If after 2 seconds, they collide. Then value of d is:
View Solution