Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
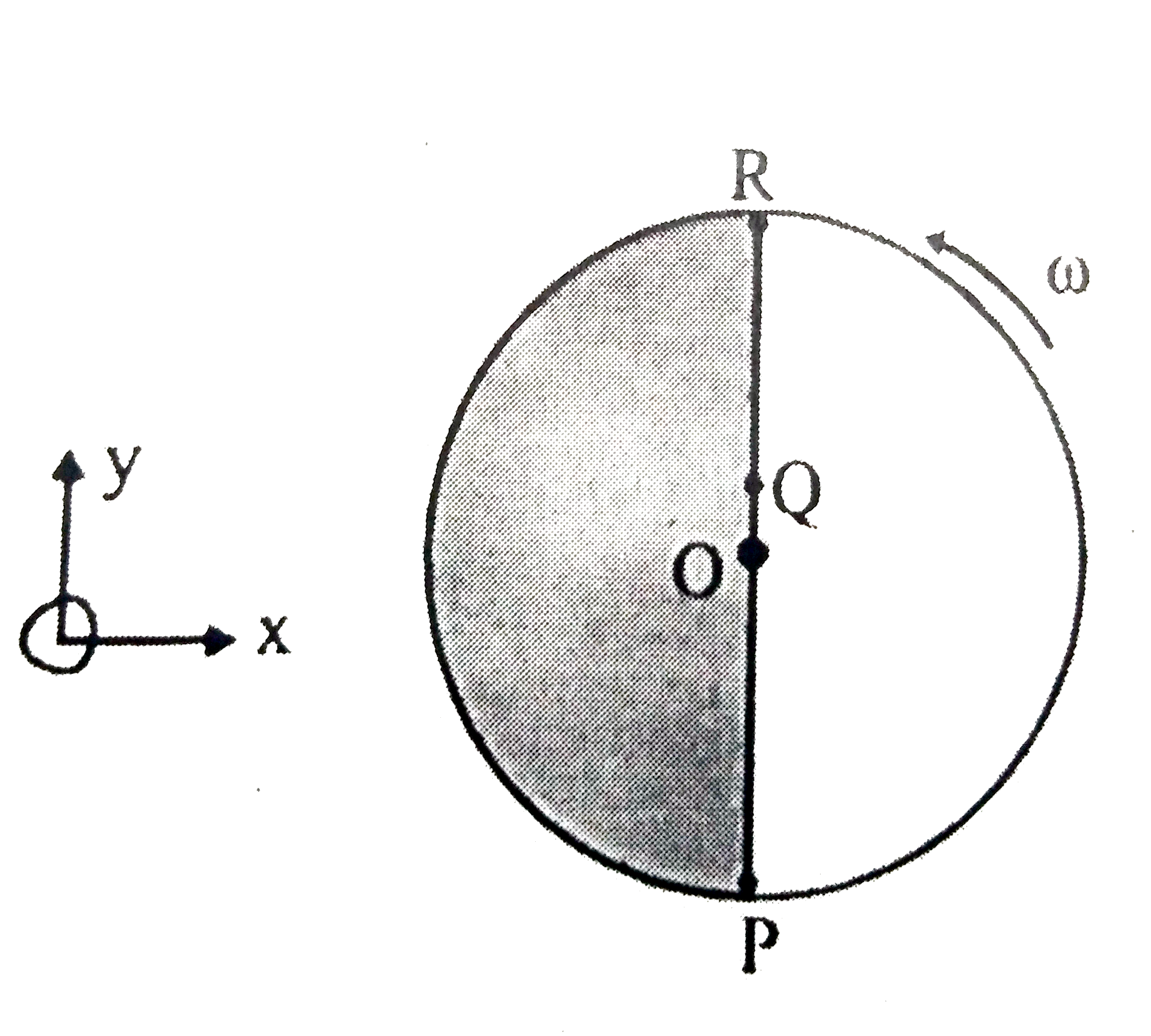
P lands in the shaded region and Q in the unshaded region
P lands in the unshaded region and Q in the shaded region
Both P and Q land in the unshaded region
Both P and Q land in the shaded region
The correct Answer is:C
At t=18×2πω=π4ω
x-coordinate of P=ωR(π4ω)=πR4>Rcos45∘.
Therefore, both particles P and Q land in unshaded region
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)
19 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its center O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 1/8 rotation, (ii) their range is less than half the disc radius, and (iii) ω remains constant throughout. Then
1.png)
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
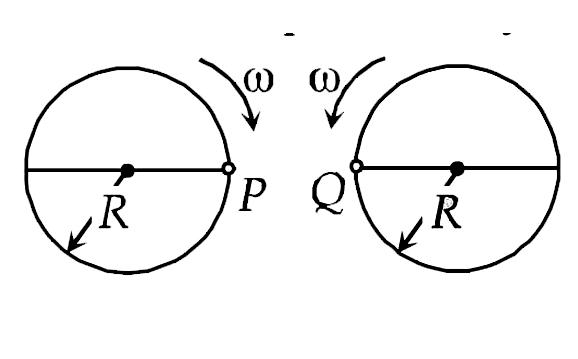
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

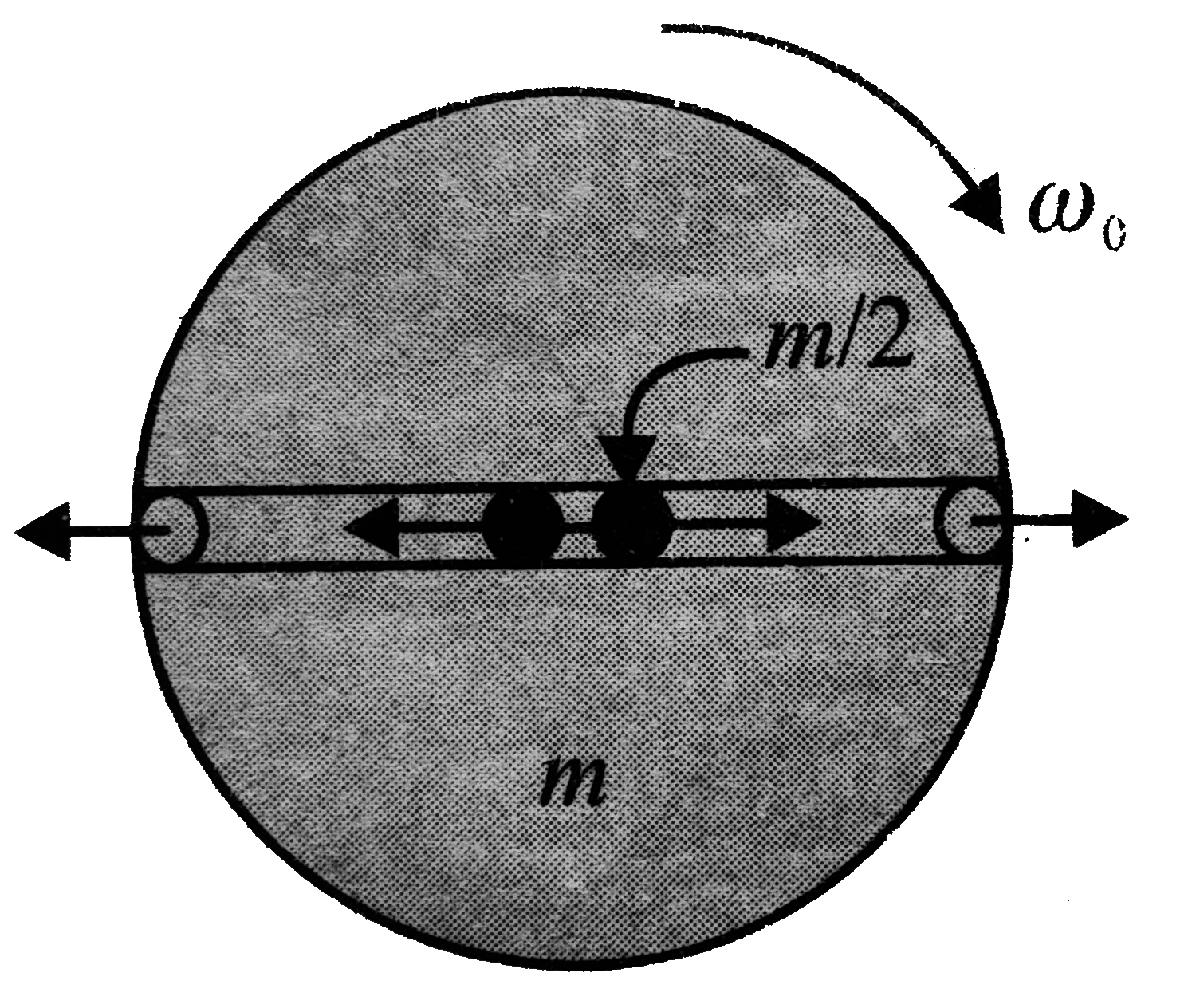
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The speed of each ball relative to the ground just after they leave the disc is
View Solution
