If a system undergoes an adiabatic change from state 1 to state 2, the work done by the gas is:
U1−U2
U2−U1
CV(T2−T1)
12(P1V2−P1V1)
The correct Answer is:A
To solve the problem of finding the work done by the gas during an adiabatic change from state 1 to state 2, we can follow these steps:
1. Understand the Adiabatic Process:
In an adiabatic process, there is no heat exchange with the surroundings. This means that the heat transfer q is equal to zero.
2. Apply the First Law of Thermodynamics:
The first law of thermodynamics states:
q=ΔU+W
where q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
3. Substitute for an Adiabatic Process:
Since q=0 for an adiabatic process, we can rewrite the equation as:
0=ΔU+W
Rearranging this gives us:
W=−ΔU
4. Express Change in Internal Energy:
The change in internal energy ΔU can be expressed as:
ΔU=U2−U1
where U1 is the internal energy at state 1 and U2 is the internal energy at state 2.
5. Substitute Change in Internal Energy into Work Equation:
Substituting ΔU into the work equation gives:
W=−(U2−U1)=U1−U2
6. Final Expression for Work Done:
Thus, the work done by the gas during the adiabatic process from state 1 to state 2 is:
W=U1−U2
Conclusion:
The work done by the gas during an adiabatic change from state 1 to state 2 is equal to the difference in internal energy, expressed as W=U1−U2.
---
In an adiabatic process, there is no heat exchange with the surroundings. This means that the heat transfer q is equal to zero.
The first law of thermodynamics states:
q=ΔU+W
where q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
Since q=0 for an adiabatic process, we can rewrite the equation as:
0=ΔU+W
Rearranging this gives us:
W=−ΔU
The change in internal energy ΔU can be expressed as:
ΔU=U2−U1
where U1 is the internal energy at state 1 and U2 is the internal energy at state 2.
Substituting ΔU into the work equation gives:
W=−(U2−U1)=U1−U2
Thus, the work done by the gas during the adiabatic process from state 1 to state 2 is:
W=U1−U2
The work done by the gas during an adiabatic change from state 1 to state 2 is equal to the difference in internal energy, expressed as W=U1−U2.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 240videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE MAIN (ARCHIVE )81videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - level-0 Short Answer Type – II24videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2)
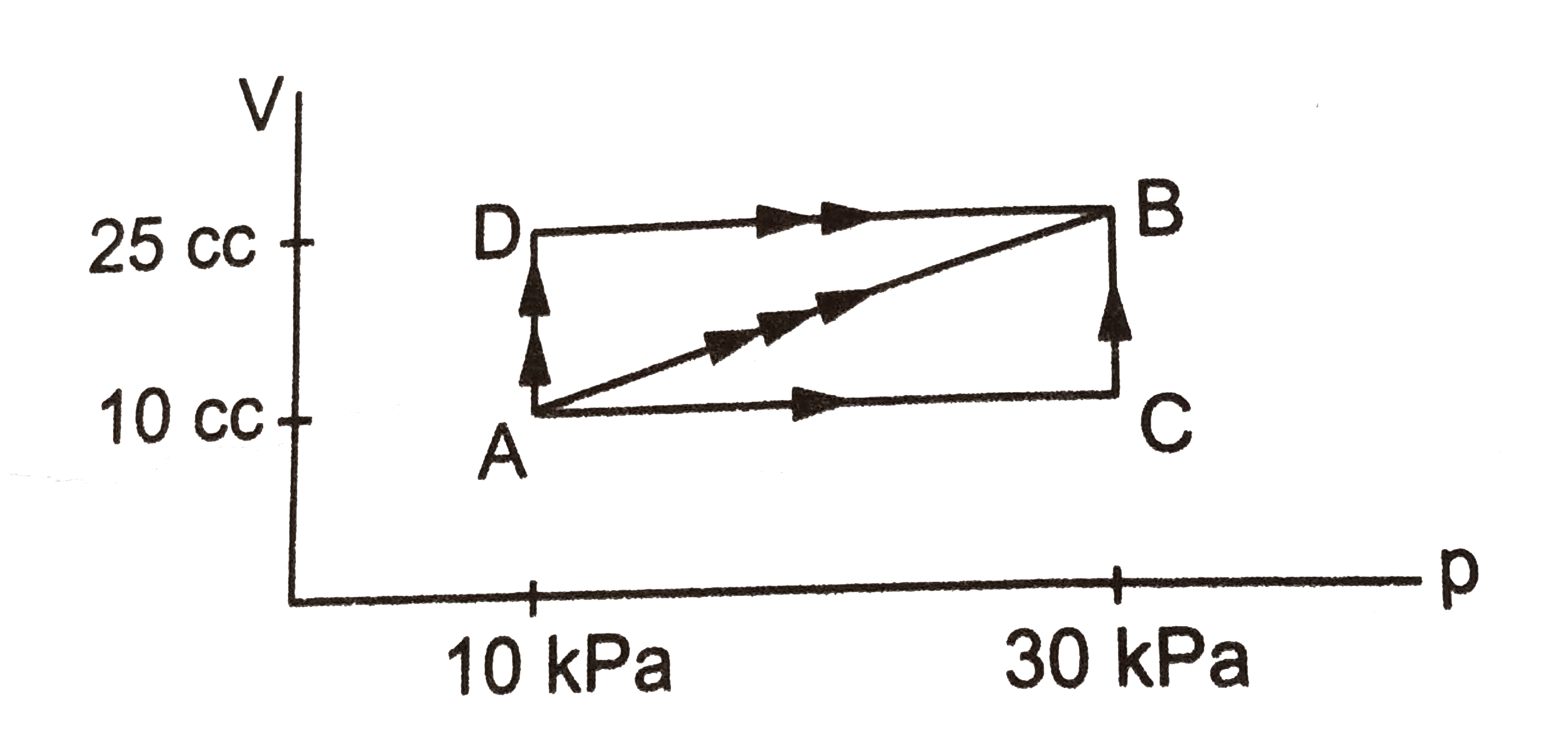
An ideal gas goes from the state i to the state ∫ as shown in .the work done by the gas during the process
 View Solution
View SolutionIn given figure, when a thermodynamic system is taken from state A to state B via path ACB,100 cal of heat given to the system and 60cal work is done by the gas. Along the path ADB, the work done by the gas is 20cal. Find the heat flowing into the system in this case?
 View Solution
View SolutionA gas undergoes change from state A to state B. In this process, the heat absorbed and work done by the gas is 5 J and 8 J, respectively. Now gas is brought back to A by another process during which 3 J of heat is evolved. In this reverse process of B to A:
View SolutionA gas undergoes expansion according to the following graph. Calculate work done by the gas
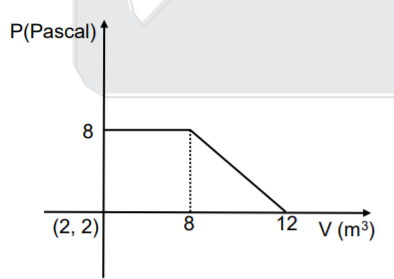 View Solution
View SolutionA gas undergoes expansion according to the following graph. Calculate work done by the gas
 View Solution
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
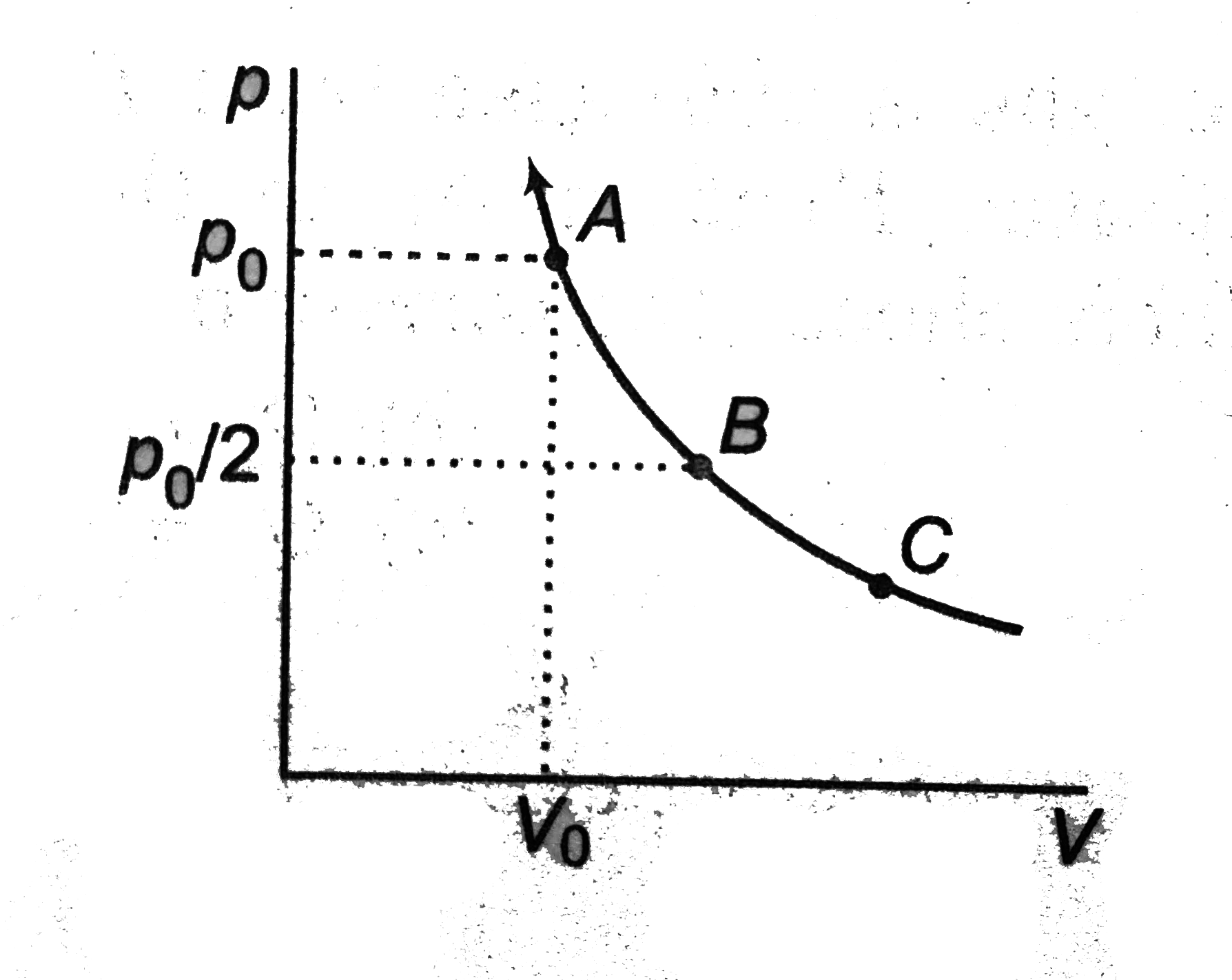 View Solution
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
 View Solution
View Solution