Two different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
(a)PA<PB and TA<TB
(b)PAPB and TA>TB
(c)PA>PB and TA<TB
(d)PA<PB and TA>TB
The correct Answer is:A
To solve the problem, we need to analyze the behavior of two different ideal diatomic gases, A and B, when they undergo different processes (adiabatic for gas A and isothermal for gas B) while reaching the same final volume.
1. Understanding the Initial Conditions:
- Both gases A and B are initially in the same state, which means they have the same initial pressure Pi and temperature Ti.
2. Final Volume:
- Both gases are expanded to the same final volume Vf.
3. Process for Gas A (Adiabatic Expansion):
- In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas undergoing adiabatic expansion, the relationship between pressure and volume can be described by the equation:
PVγ=constant
where γ (gamma) is the heat capacity ratio Cp/Cv. For diatomic gases, γ is typically 75 or 1.4.
4. Final Pressure and Temperature for Gas A:
- Since gas A expands adiabatically to a larger volume, its final pressure PA will be lower than its initial pressure Pi.
- The final temperature TA will also decrease due to the adiabatic expansion, as the internal energy of the gas decreases.
5. Process for Gas B (Isothermal Expansion):
- In an isothermal process, the temperature remains constant. The relationship between pressure and volume for an ideal gas is given by:
PV=nRT
where n is the number of moles and R is the ideal gas constant.
- Since gas B is undergoing isothermal expansion, its final pressure PB will be lower than its initial pressure Pi, but the temperature TB will remain equal to the initial temperature Ti.
6. Comparing Final States:
- From the adiabatic expansion of gas A, we have:
PA<PiandTA<Ti
- From the isothermal expansion of gas B, we have:
PB<PiandTB=Ti
7. Conclusion:
- Since both gases are at the same final volume and gas A has undergone a temperature drop, we can conclude:
PA<PBandTA<TB
- Therefore, the correct option is C: PA<PB and TA<TB.
- Both gases A and B are initially in the same state, which means they have the same initial pressure Pi and temperature Ti.
- Both gases are expanded to the same final volume Vf.
- In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas undergoing adiabatic expansion, the relationship between pressure and volume can be described by the equation:
PVγ=constant
where γ (gamma) is the heat capacity ratio Cp/Cv. For diatomic gases, γ is typically 75 or 1.4.
- Since gas A expands adiabatically to a larger volume, its final pressure PA will be lower than its initial pressure Pi.
- The final temperature TA will also decrease due to the adiabatic expansion, as the internal energy of the gas decreases.
- In an isothermal process, the temperature remains constant. The relationship between pressure and volume for an ideal gas is given by:
PV=nRT
where n is the number of moles and R is the ideal gas constant.
- Since gas B is undergoing isothermal expansion, its final pressure PB will be lower than its initial pressure Pi, but the temperature TB will remain equal to the initial temperature Ti.
- From the adiabatic expansion of gas A, we have:
PA<PiandTA<Ti
- From the isothermal expansion of gas B, we have:
PB<PiandTB=Ti
- Since both gases are at the same final volume and gas A has undergone a temperature drop, we can conclude:
PA<PBandTA<TB
- Therefore, the correct option is C: PA<PB and TA<TB.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 240videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE MAIN (ARCHIVE )81videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - level-0 Short Answer Type – II24videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
Similar Questions
Two gases have the same initial pressure, volume and temperature. They expand to the same final volume, one adiabatically and the other isothermally
View SolutionTwo samples 1 and 2 are initially kept in the same state. The sample 1 is expanded through an isothermal process where as sample 2 through an adiabatic process upto the same final volume. The final temperature in process 1 and 2 are T1 and T2 respectively, then
View Solution
Knowledge Check
- Question 1 - Select One
Three vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
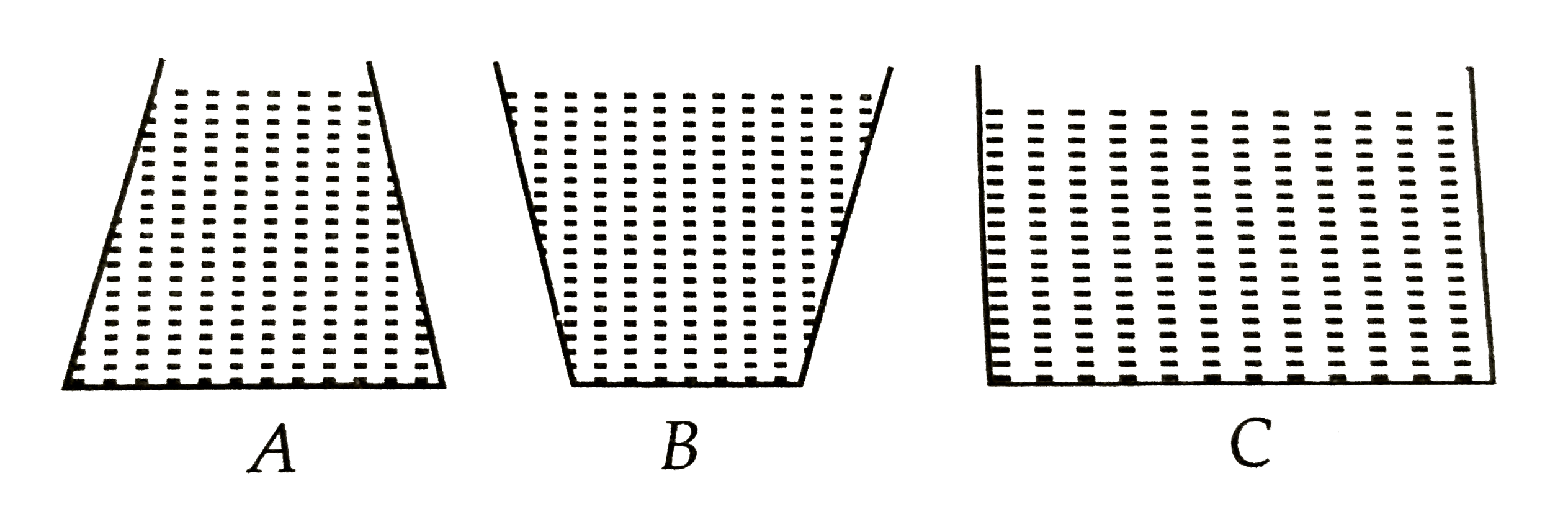 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC - Question 2 - Select One
Two samples, A and B of a gas at the same initial temperature and pressure are compressed from volume V to V/2, A isothermally and B adiabatically. The final pressure of A will be
Agreater than that of BBequal to that of BCless than of BDtwice that of B
Two samples 1 and 2 are initially kept in the same state. The sample 1 is expanded through an isothermal process where as sample 2 through an adiabatic process upto the same final volume. The final temperature in process 1 and 2 are T1 and T2 respectively, then
View SolutionTwo sample A and B of a gas initially at the same pressure and temperature are compressed from volume V to V/2 (A isothermally and B adiabatically). The final pressure of A is
View SolutionEqual molecules of two gases are in thermal equilibrium. If Pa,PbandVa,Vb are their respective pressures and volumes, then which of the following relation is true?
View SolutionThe value of Cp−Cv is 1.09R for a gas sample in state A and is 1.00R in state B. Let AA,TB denote the temperature and pA and PB denote the pressure of the states A and B respectively. Then
View SolutionTen moles of a diatomic perfect gas are allowed to expand at constant pressure. The initial volume and temperature are V0 and T0 respectively. If 72RT0 heat is transferred to the gas, then the final volume and temperature are
View SolutionThere are two statement of same gas initially under similar initial state. Gases of both the samples are expanded. I s t sample using reversible isothermal process and I I n d sample using reversible adiabatic process till final pressure of both the samples becomes half of initial pressure. Then:
View Solution

