The number density of molecules of a gas depends on their distance r from the origin as, n(r)=n0e−αr4. Then the total number of molecules is proportional to :
n0α−3/4
√n0α1/2
n0α1/4
n0α−3
The correct Answer is:A
To solve the problem, we need to find the total number of molecules based on the given number density function n(r)=n0e−αr4. The total number of molecules can be found by integrating the number density over the entire volume of the gas.
1. Understanding Number Density:
The number density of the gas is given by:
n(r)=n0e−αr4
where n0 is a constant and α is a positive constant.
2. Volume Element in Spherical Coordinates:
To find the total number of molecules, we need to integrate the number density over the volume. In spherical coordinates, the volume element dv is given by:
dv=4πr2dr
3. Setting Up the Integral:
The total number of molecules N is given by the integral of the number density times the volume element:
N=∫∞0n(r)dv=∫∞0n0e−αr4⋅4πr2dr
Thus, we can rewrite the integral as:
N=4πn0∫∞0r2e−αr4dr
4. Changing Variables:
To evaluate the integral, we can use a substitution. Let:
u=αr4⟹du=4αr3dr⟹dr=du4αr3
We also need to express r2 in terms of u:
r2=(uα)1/2⋅(1α)1/4
The limits of integration remain from 0 to ∞.
5. Evaluating the Integral:
The integral becomes:
∫∞0r2e−αr4dr=∫∞0(uα)1/2e−u⋅du4α(uα)3/4=14α3/4∫∞0u1/2e−udu
The integral ∫∞0u1/2e−udu is a known result and equals Γ(3/2)=√π2.
6. Final Expression:
Substituting back, we have:
N=4πn0⋅14α3/4⋅√π2=n0⋅π3/22α3/4
Therefore, the total number of molecules N is proportional to:
N∝n0α−3/4
Conclusion:
The total number of molecules is proportional to n0α−3/4.
The number density of the gas is given by:
n(r)=n0e−αr4
where n0 is a constant and α is a positive constant.
To find the total number of molecules, we need to integrate the number density over the volume. In spherical coordinates, the volume element dv is given by:
dv=4πr2dr
The total number of molecules N is given by the integral of the number density times the volume element:
N=∫∞0n(r)dv=∫∞0n0e−αr4⋅4πr2dr
Thus, we can rewrite the integral as:
N=4πn0∫∞0r2e−αr4dr
To evaluate the integral, we can use a substitution. Let:
u=αr4⟹du=4αr3dr⟹dr=du4αr3
We also need to express r2 in terms of u:
r2=(uα)1/2⋅(1α)1/4
The limits of integration remain from 0 to ∞.
The integral becomes:
∫∞0r2e−αr4dr=∫∞0(uα)1/2e−u⋅du4α(uα)3/4=14α3/4∫∞0u1/2e−udu
The integral ∫∞0u1/2e−udu is a known result and equals Γ(3/2)=√π2.
Substituting back, we have:
N=4πn0⋅14α3/4⋅√π2=n0⋅π3/22α3/4
Therefore, the total number of molecules N is proportional to:
N∝n0α−3/4
The total number of molecules is proportional to n0α−3/4.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 240videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
Similar Questions
The mean free path of molecules of a gas (radius r) is inversely proportional to
View SolutionA : Number of air molecules in a room in winter is more than the number of molecules in the same room in summer.
R : At a given pressure and volume, the number of molecules of a given mass of a gas is directly proportional to the absolute temperature.View SolutionThe electric field inside a sphere having charge density related to the distance from the centre asρ=αr (α is a constant) is :
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
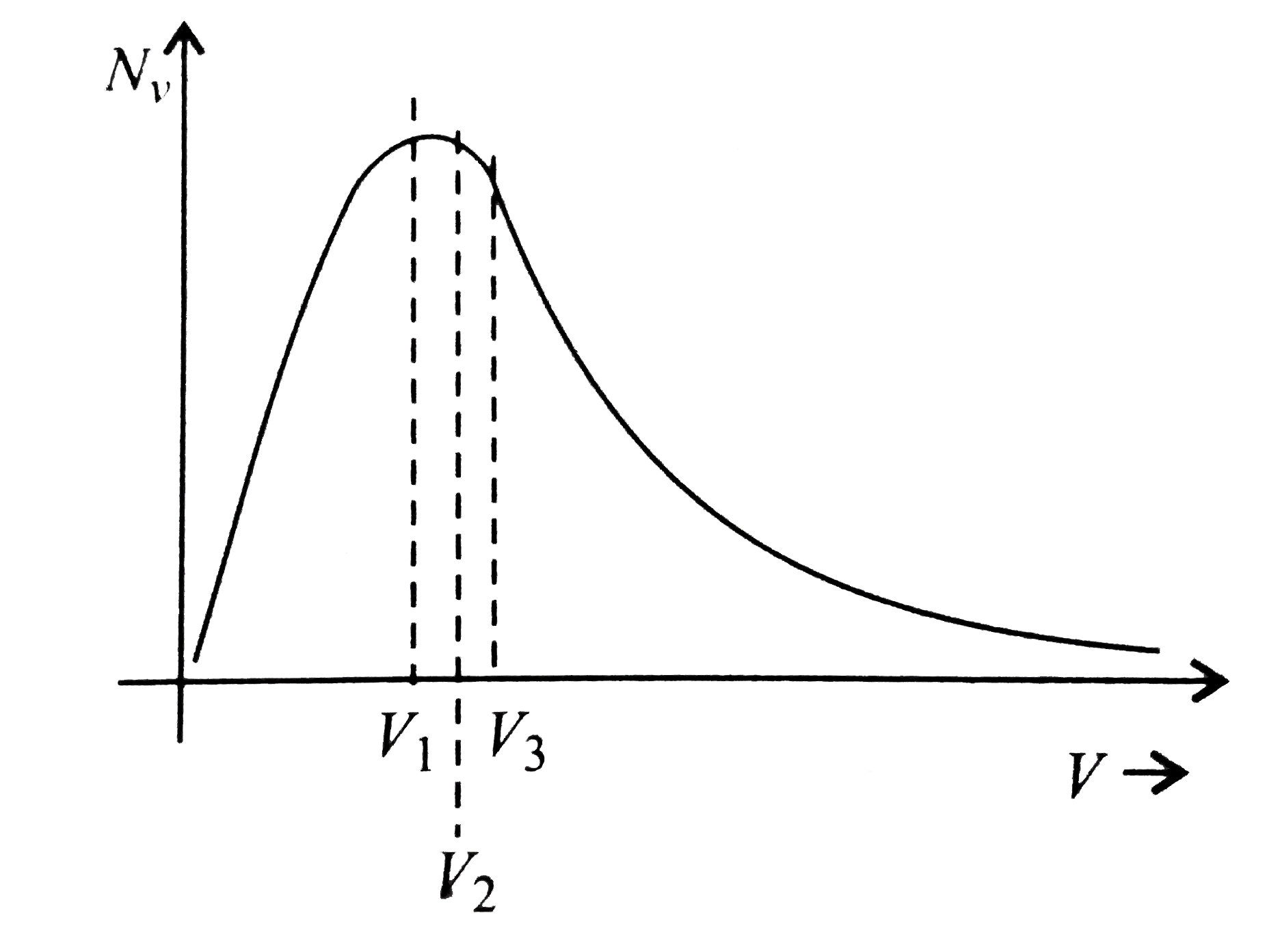
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a areView SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
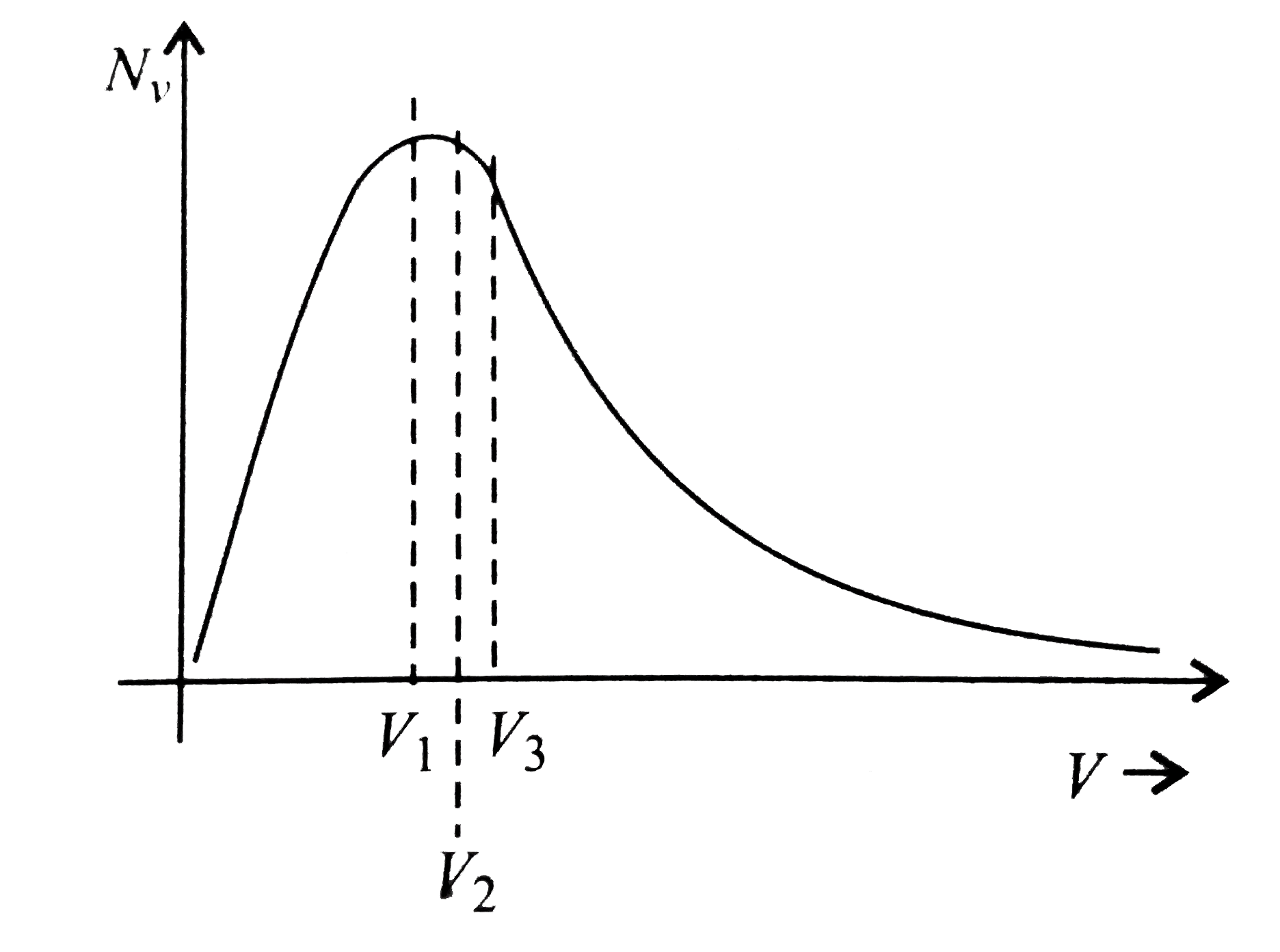
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b areView SolutionLet f(n)=n∑r=0n∑k=r(kr). Find the total number of divisors of f(9).
View SolutionThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r)=J0(1−rR) . The total current in the radial regon r = 0 to r=R4 will be :
View SolutionA large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 View Solution
View SolutionA small piece of mass m moves in such a way the P.E. =−12mkr2. Where k is a constant and r is the distance of the particle from origin. Assuming Bohr's model of quantization of angular momentum and circular orbit, r is directly proportional to :
(a)n2
(b)n
(c)√n
(d)none of theseView Solution

