Charge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

ρ0πR3
2ρ0πR2
3ρ0πR2
4ρ0πeR2
The correct Answer is:B
Step by step video & image solution for Charge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionMass density of sphere of radius R is Kr2. Where K is constant and r is distance from centre. A particle is moving near surface of sphere along circular path of radius R with time period T. Then
View Solution
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
Mass density of sphere of radius R is Kr2. Where K is constant and r is distance from centre. A particle is moving near surface of sphere along circular path of radius R with time period T. Then
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionLet a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
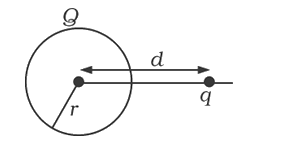
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View Solution
