The system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.
(a)The system performs, SHM with time period π10s
(b)The block of mass 3 kg perform SHM with amplitude 4 cm
(c)The block of mass 6 kg will have maximum momentum of 2.40 kg m//s
(d)The time periods of two blocks are in the ratio 1:√2
The correct Answer is:ABC
T=2π√μk: μ=(m1m2m1+m2) : A=6cm×(mm2m1+m2)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (1)75videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
The system shown in the figure can move on a smooth surface. They are initially compressed by 6cm and then released, then choose the correct options.
(a) The system performs, SHM with time period π10s
(b) The block of mass 3kg perform SHM with amplitude 4cm
( c) The block of mass 6kg will have maximum momentum of 2.40kg−m/s
(d) The time periods of two blocks are in the ratio of 1:√2View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.
(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionFor the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is :
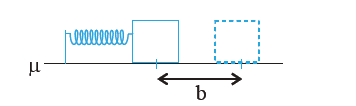View Solutionm1 & m2 are connected with a light inextensible string with m1 lying on smooth table and m2 hanging as shown in figure. m1 is also connected to a light spring which is initially unstretched an the system is released from rest.
View SolutionIn the figure shown, all surfaces are smooth and force constant of spring is 10N/m. Block of mass (2 kg) is attaced with the spring. The spring is compressed by (2m) and then released. Find the maximum distance d travelled by the block over the inclined plane. Take g=10m/s2.
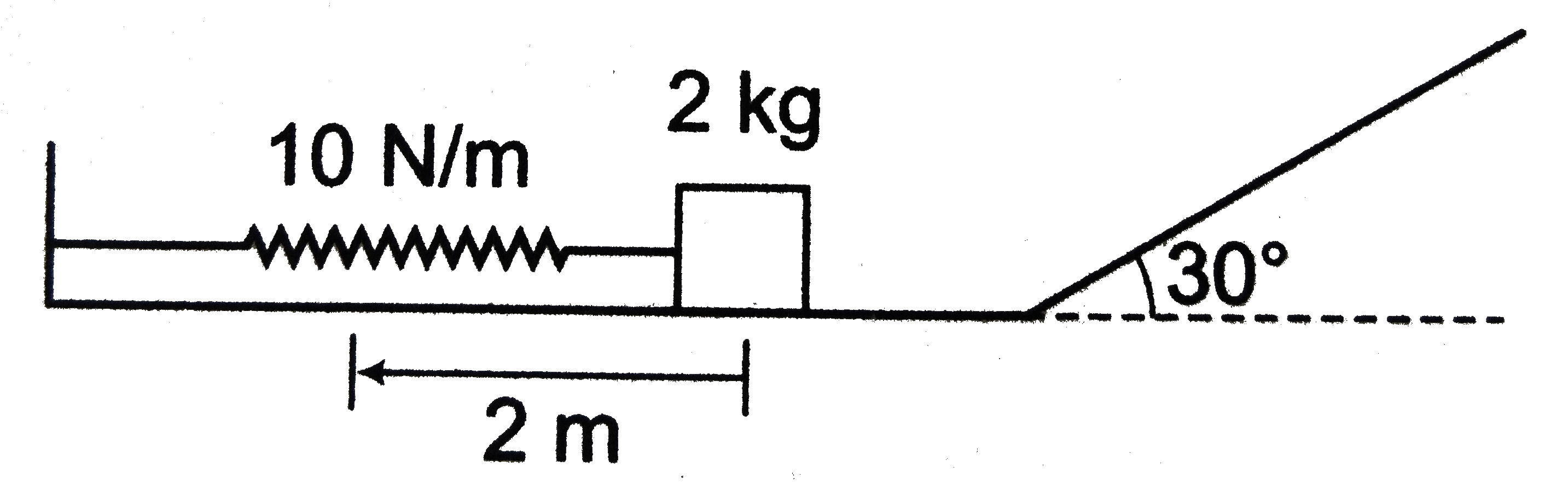.View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck
View SolutionTwo identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is
View SolutionA block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
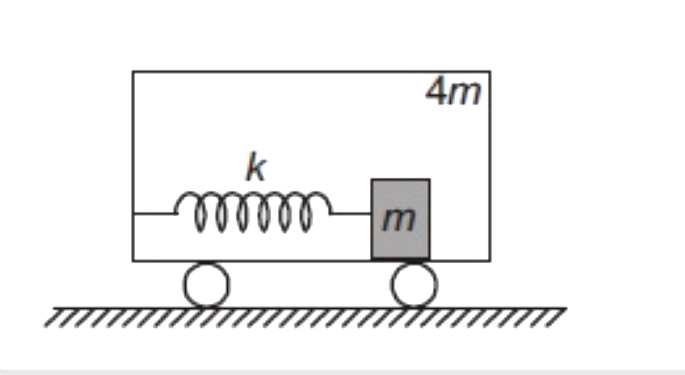View Solution