A ball of radius 11 cm and mass 8 kg rolls from rest down a ramp of length 2m. The ramp is inclined at 35° to the horizontal. When the ball reaches the bottom, its velocity is (sin 35° = 0.57)?
2 m/s
5 m/s
4 m/s
6 m/s
The correct Answer is:C
To solve the problem of a ball rolling down an inclined ramp, we will use the principle of conservation of energy. The potential energy at the top of the ramp will be converted into both translational and rotational kinetic energy at the bottom.
1. Identify the Given Values:
- Mass of the ball, m=8kg
- Radius of the ball, r=11cm=0.11m
- Length of the ramp, L=2m
- Angle of inclination, θ=35∘
- Gravitational acceleration, g=9.8m/s2
- sin(35∘)=0.57
2. Calculate the Height of the Ramp:
The height H of the ramp can be calculated using the sine function:
H=Lsin(θ)=2×sin(35∘)=2×0.57=1.14m
3. Write the Conservation of Energy Equation:
The potential energy at the top of the ramp is converted into kinetic energy at the bottom. The equation is:
mgh=12mv2+12Iω2
For a solid sphere, the moment of inertia I is given by:
I=25mr2
The relationship between linear velocity v and angular velocity ω is:
ω=vr
4. Substituting the Moment of Inertia:
Substitute I into the energy equation:
mgh=12mv2+12(25mr2)(v2r2)
Simplifying this gives:
mgh=12mv2+15mv2=(12+15)mv2=710mv2
5. Canceling Mass and Rearranging:
Cancel m from both sides:
gh=710v2
Rearranging gives:
v2=10gh7
6. Substituting Values:
Substitute g=9.8m/s2 and h=1.14m:
v2=10×9.8×1.147
Calculate the right-hand side:
v2=111.127≈15.87
7. Taking the Square Root:
Finally, take the square root to find v:
v≈√15.87≈4m/s
Final Answer:
The velocity of the ball when it reaches the bottom of the ramp is approximately 4m/s.
- Mass of the ball, m=8kg
- Radius of the ball, r=11cm=0.11m
- Length of the ramp, L=2m
- Angle of inclination, θ=35∘
- Gravitational acceleration, g=9.8m/s2
- sin(35∘)=0.57
The height H of the ramp can be calculated using the sine function:
H=Lsin(θ)=2×sin(35∘)=2×0.57=1.14m
The potential energy at the top of the ramp is converted into kinetic energy at the bottom. The equation is:
mgh=12mv2+12Iω2
For a solid sphere, the moment of inertia I is given by:
I=25mr2
The relationship between linear velocity v and angular velocity ω is:
ω=vr
Substitute I into the energy equation:
mgh=12mv2+12(25mr2)(v2r2)
Simplifying this gives:
mgh=12mv2+15mv2=(12+15)mv2=710mv2
Cancel m from both sides:
gh=710v2
Rearranging gives:
v2=10gh7
Substitute g=9.8m/s2 and h=1.14m:
v2=10×9.8×1.147
Calculate the right-hand side:
v2=111.127≈15.87
Finally, take the square root to find v:
v≈√15.87≈4m/s
The velocity of the ball when it reaches the bottom of the ramp is approximately 4m/s.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE E
10 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
A disc rolls down a plane of length L and inclined at angle θ, without slipping. Its velocity on reaching the bottom will be :-
View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
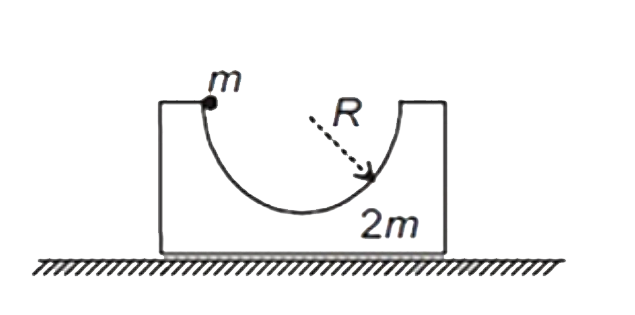
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is

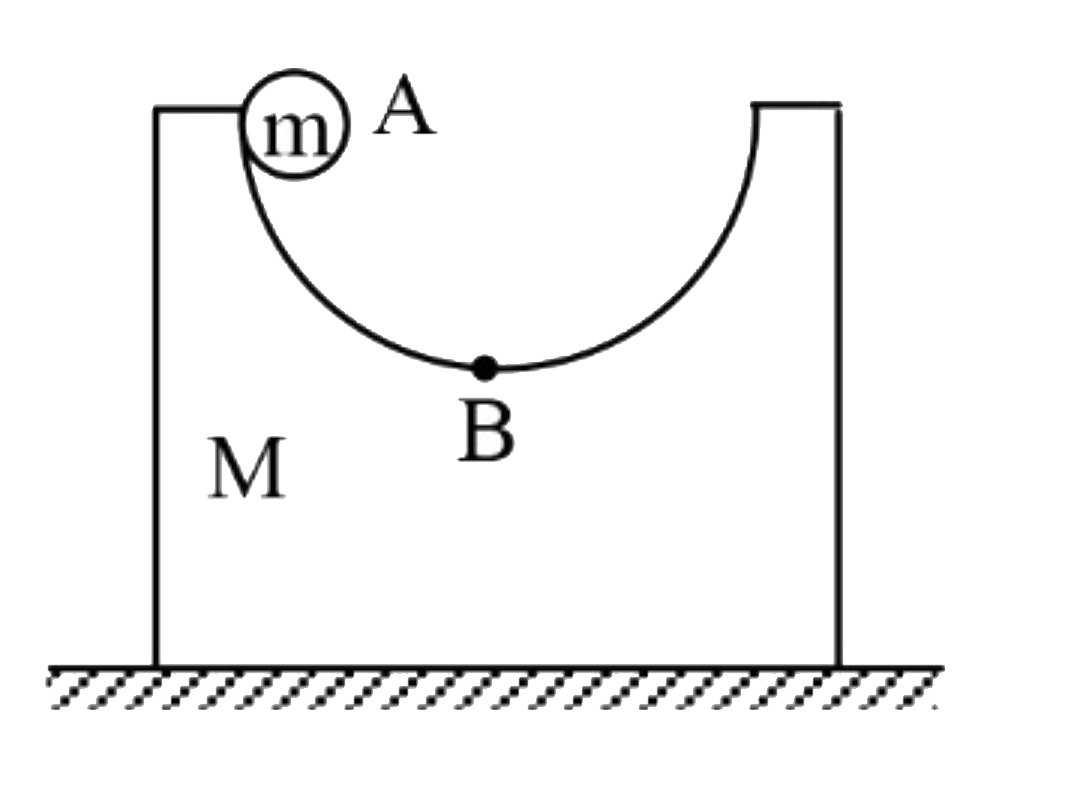
View SolutionA block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g=10ms−2)
View Solution
