The (x,y) co-ordinates of the corners of a square plate are (0,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)
acos(πx/2L)cos(πy/2L)
asin(πx/L)sin(πy/L)
asin(πx/L)sin(2πy/L)
acos(2πx/L)sin(2πy/L)
The correct Answer is:B, C
To solve the problem of finding the possible expressions for the displacement u(x,y) of a clamped square plate with corners at coordinates (0,0), (L,0), (L,L), and (0,L), we need to ensure that the displacement at the edges of the plate is zero.
1. Understanding the Boundary Conditions:
- Since the edges of the plate are clamped, the displacement u(x,y) must be zero along the edges of the square.
- The edges are defined by:
- y=0 (bottom edge)
- x=L (right edge)
- y=L (top edge)
- x=0 (left edge)
2. Examining Possible Expressions:
- We need to check each proposed expression for u(x,y) to see if it satisfies the boundary conditions.
3. Checking Expression A:
- u(x,y)=acos(πx2L)cos(πy2L)
- For y=0:
u(x,0)=acos(πx2L)cos(0)=acos(πx2L)
- This is not zero for x varying from 0 to L. Thus, Expression A is not valid.
4. Checking Expression B:
- u(x,y)=asin(πxL)sin(πyL)
- For y=0:
u(x,0)=asin(πxL)sin(0)=0
- For x=L:
u(L,y)=asin(π)sin(πyL)=0
- For y=L:
u(x,L)=asin(πxL)sin(π)=0
- For x=0:
u(0,y)=asin(0)sin(πyL)=0
- Expression B is valid.
5. Checking Expression C:
- u(x,y)=asin(πxL)sin(2πyL)
- For y=0:
u(x,0)=asin(πxL)sin(0)=0
- For x=L:
u(L,y)=asin(π)sin(2πyL)=0
- For y=L:
u(x,L)=asin(πxL)sin(2π)=0
- For x=0:
u(0,y)=asin(0)sin(2πyL)=0
- Expression C is also valid.
6. Checking Expression D:
- u(x,y)=acos(2πxL)sin(2πyL)
- For y=0:
u(x,0)=acos(2πxL)sin(0)=0
- For x=L:
u(L,y)=acos(2π)sin(2πyL)=asin(2πyL)
- This is not zero for y varying from 0 to L. Thus, Expression D is not valid.
Conclusion:
The valid expressions for u(x,y) that satisfy the boundary conditions are B and C.
- Since the edges of the plate are clamped, the displacement u(x,y) must be zero along the edges of the square.
- The edges are defined by:
- y=0 (bottom edge)
- x=L (right edge)
- y=L (top edge)
- x=0 (left edge)
- We need to check each proposed expression for u(x,y) to see if it satisfies the boundary conditions.
- u(x,y)=acos(πx2L)cos(πy2L)
- For y=0:
u(x,0)=acos(πx2L)cos(0)=acos(πx2L)
- This is not zero for x varying from 0 to L. Thus, Expression A is not valid.
- u(x,y)=asin(πxL)sin(πyL)
- For y=0:
u(x,0)=asin(πxL)sin(0)=0
- For x=L:
u(L,y)=asin(π)sin(πyL)=0
- For y=L:
u(x,L)=asin(πxL)sin(π)=0
- For x=0:
u(0,y)=asin(0)sin(πyL)=0
- Expression B is valid.
- u(x,y)=asin(πxL)sin(2πyL)
- For y=0:
u(x,0)=asin(πxL)sin(0)=0
- For x=L:
u(L,y)=asin(π)sin(2πyL)=0
- For y=L:
u(x,L)=asin(πxL)sin(2π)=0
- For x=0:
u(0,y)=asin(0)sin(2πyL)=0
- Expression C is also valid.
- u(x,y)=acos(2πxL)sin(2πyL)
- For y=0:
u(x,0)=acos(2πxL)sin(0)=0
- For x=L:
u(L,y)=acos(2π)sin(2πyL)=asin(2πyL)
- This is not zero for y varying from 0 to L. Thus, Expression D is not valid.
The valid expressions for u(x,y) that satisfy the boundary conditions are B and C.
Topper's Solved these Questions
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE ADVANCED ARCHIVE LEVEL 2 (PARAGRAPH TYPE)
Explore 6 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE ADVANCED ARCHIVE LEVEL 2 (MATRIX MATCH TYPE)
Explore 3 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE ADVANCED ARCHIVE LEVEL 2
Explore 32 Videos
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:IN - CHAPTER EXERCISE - B
Explore 10 Videos
- WORK ENERGY AND POWER Book:VMC MODULES ENGLISHChapter:WORK ENERGY AND POWER Exercise:IMPECCABLE
Explore 54 Videos
Similar Questions
The (x,y) co-ordinates of the corners of a square plate are (0,0),(L,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)
View SolutionThe figure shows an isosceles triangle plate of mass M and base L.
The angle at the apex is 90∘. The apex lies at the origin and the base is parallel to X−axis.
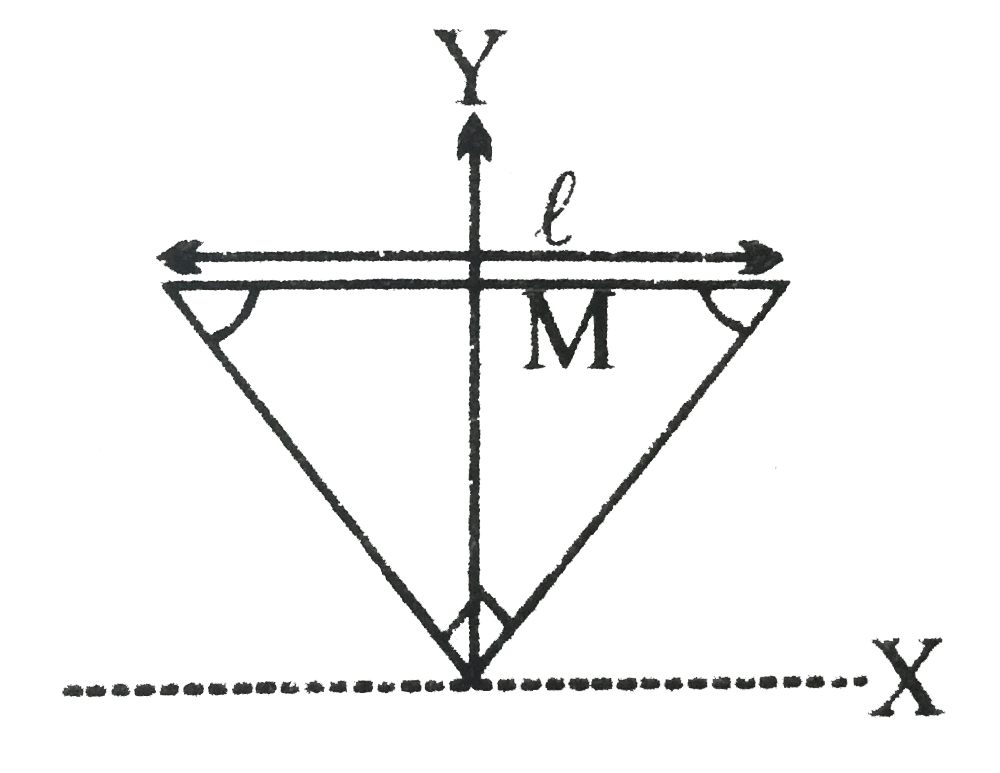
The moment of inertia of the plate about the y−axis is
View Solution
Knowledge Check
If the corner points of the feasible region for an L.P.P. are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5), then the minimum value of the objective function F=4x+6y occurs at
AA) (0, 2) onlyBB) (3, 0) onlyCC) the mid-point of the line segment joining the point (0, 2) and (3, 0) onlyDD) every point on the line segment joining the point (0, 2) and (3, 0)
For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
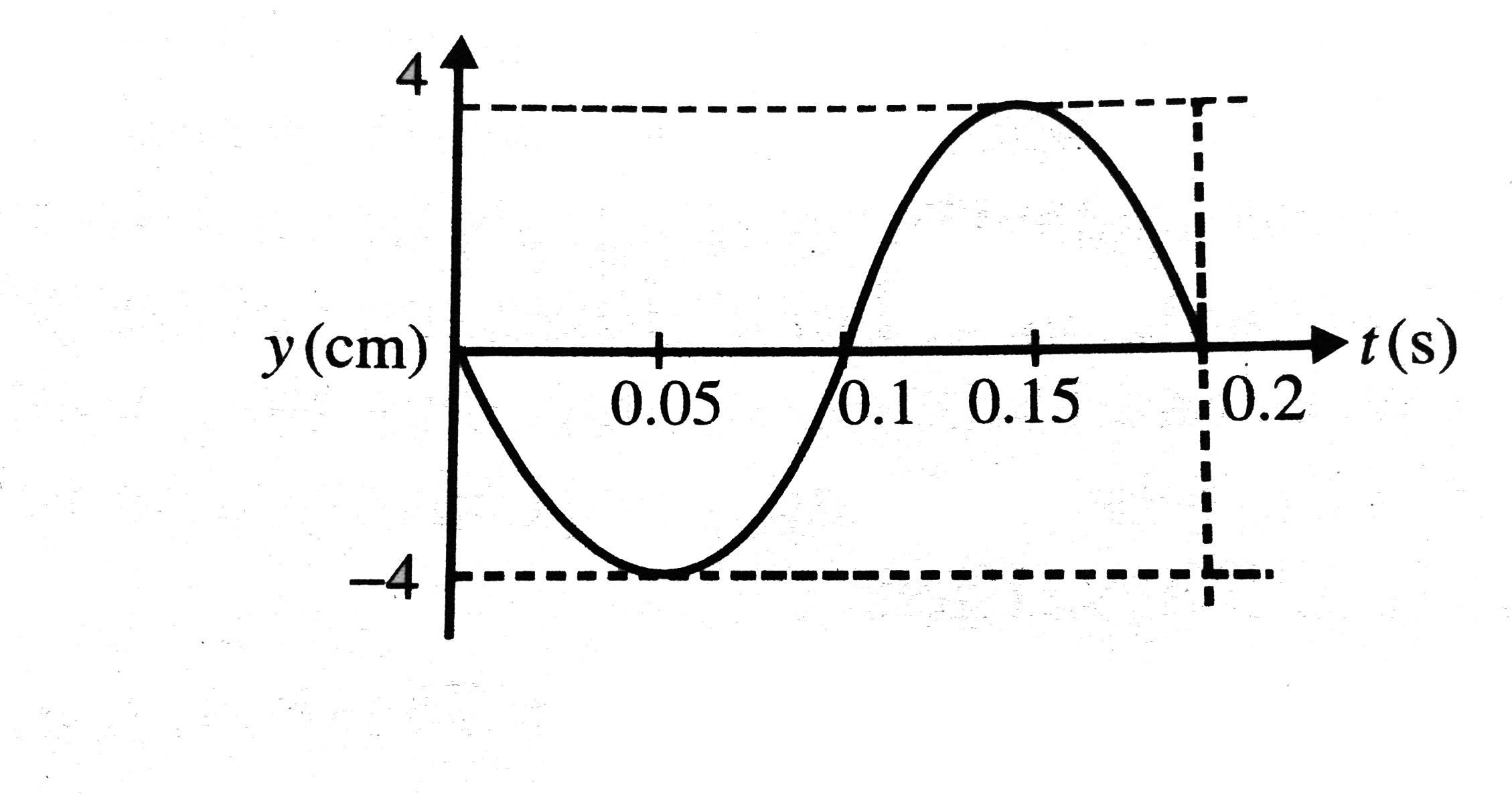
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
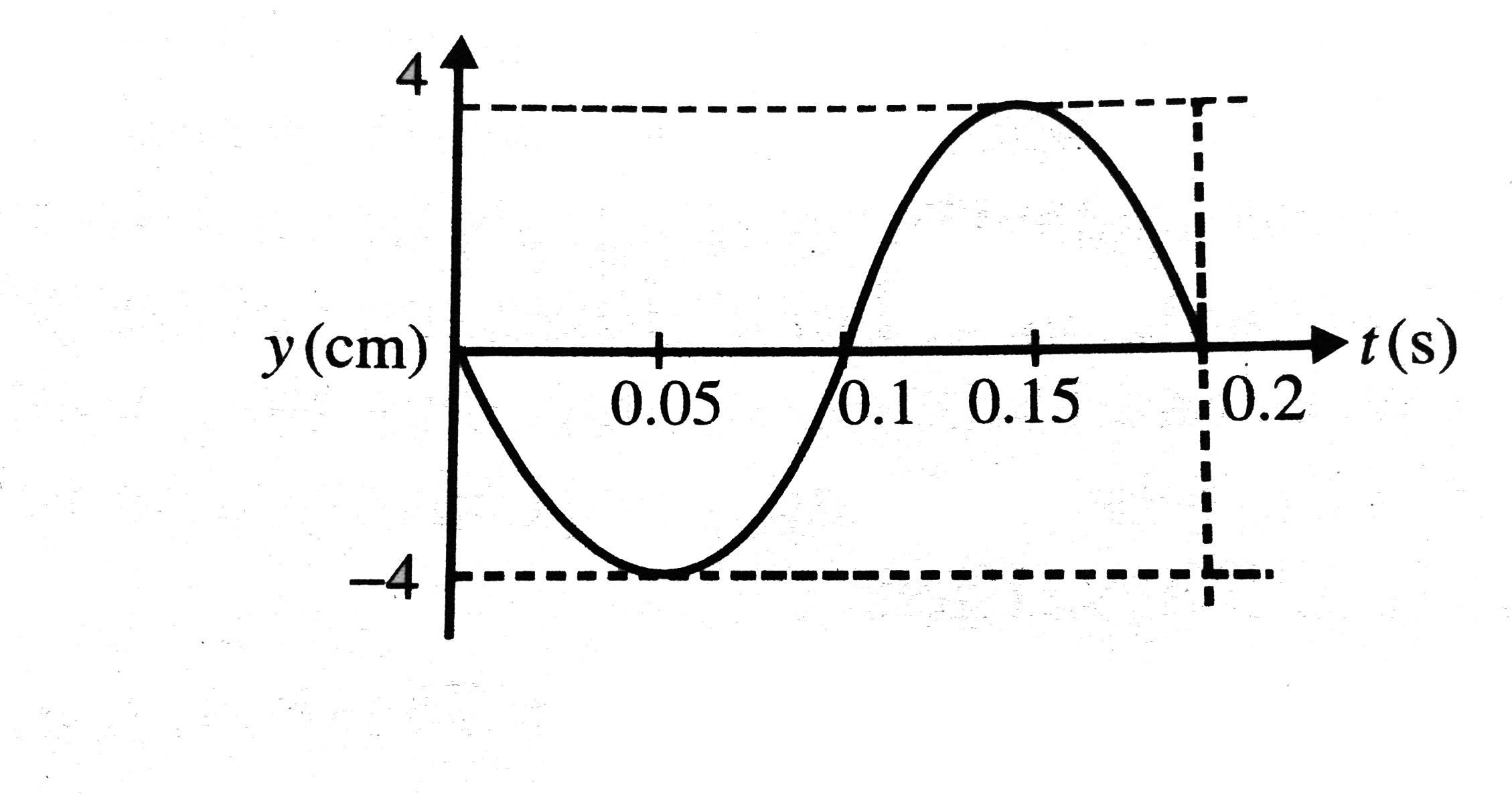
View SolutionThe standing wave in a medium is expressed as y=0.2sin(0.8x)cos(3000t)m. The distance between any two consecutive points of minimum of maximum displacement is
View Solutionx and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The path of the particle is a…….
View SolutionA standing wave is represeneted by y=asin(100t)cos(0.01)x in second and x is in ,metre. Velocity of wave is
View Solution_E01_208_Q01.png)
A metallic plate having shap of a square is suspended as shown in figure. The plate is made to dip iin water such that level of water is well above that of the plate. The point x is then slowly raised at constant velocity sketch the variation T in string with the displacement S of point x.
View Solutionx and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The distance travelled by the particle in a time from t=0 to t=2s is ………m
View Solution
