The following equations represent transverse waves :
z1=Acos(kx−ωt),
z2=Acos(kx+ωt), z3=Acos(ky−ωt)
Identify the combination (s) of the waves which will produce (i) standing wave(s), (ii) a wave travelling in the direction making an angle of 45∘ with the positive x and positive y axes. In each case, find the positions at which the resultant intensity is always zero.
The correct Answer is:(i) z2&z2,x=(2n+1)π2k where n=0,1,2,3,. . .
(ii) z1&z3,(x−y)=(2n+1)kπ where n=0,1,2, . . .
To solve the problem, we need to analyze the given wave equations and determine the combinations that produce standing waves and waves traveling at a 45-degree angle. Let's break it down step by step.
Step 1: Identify the Wave Equations
The given wave equations are:
1. z1=Acos(kx−ωt)
2. z2=Acos(kx+ωt)
3. z3=Acos(ky−ωt)
Step 2: Determine the Combination for Standing Waves
Standing waves are formed by the superposition of two waves traveling in opposite directions.
- Combination for Standing Waves:
The waves z1 and z2 are traveling in opposite directions along the x-axis. Therefore, they will produce a standing wave.
Step 3: Superimpose the Waves
Using the principle of superposition, we can add z1 and z2:
z=z1+z2=Acos(kx−ωt)+Acos(kx+ωt)
Using the trigonometric identity cosA+cosB=2cos(A+B2)cos(A−B2):
z=2Acos(kx)cos(ωt)
Step 4: Find the Resultant Intensity
The intensity I is proportional to the square of the amplitude R:
I∝R2=(2Acos(kx))2=4A2cos2(kx)
For the intensity to be zero:
cos2(kx)=0⟹cos(kx)=0
This occurs when:
kx=(n+12)π(n=0,1,2,…)
Thus, the positions where the intensity is always zero are:
x=(2n+1)π2k(n=0,1,2,…)
Step 5: Determine the Combination for Waves Traveling at 45 Degrees
To find a wave traveling at a 45-degree angle, we need to consider the waves z1 and z3:
- Combination for 45-degree Wave:
z1 travels in the x-direction, and z3 travels in the y-direction. Their combination will yield a wave traveling at a 45-degree angle.
Step 6: Superimpose the Waves
Using the principle of superposition again:
z=z1+z3=Acos(kx−ωt)+Acos(ky−ωt)
Using the trigonometric identity:
z=2Acos(kx+ky−2ωt2)cos(kx−ky2)
Step 7: Find the Resultant Intensity
The intensity I is given by:
I∝(2Acos(kx−ky2))2=4A2cos2(kx−ky2)
For the intensity to be zero:
cos2(kx−ky2)=0⟹cos(kx−ky2)=0
This occurs when:
kx−ky2=(n+12)π(n=0,1,2,…)
Thus, the positions where the intensity is always zero are:
kx−ky=(2n+1)π(n=0,1,2,…)
Summary of Results
1. Standing Waves: Formed by z1 and z2.
- Intensity is zero at x=(2n+1)π2k.
2. Waves at 45 Degrees: Formed by z1 and z3.
- Intensity is zero at kx−ky=(2n+1)π.
The given wave equations are:
1. z1=Acos(kx−ωt)
2. z2=Acos(kx+ωt)
3. z3=Acos(ky−ωt)
Standing waves are formed by the superposition of two waves traveling in opposite directions.
The waves z1 and z2 are traveling in opposite directions along the x-axis. Therefore, they will produce a standing wave.
Using the principle of superposition, we can add z1 and z2:
The intensity I is proportional to the square of the amplitude R:
To find a wave traveling at a 45-degree angle, we need to consider the waves z1 and z3:
z1 travels in the x-direction, and z3 travels in the y-direction. Their combination will yield a wave traveling at a 45-degree angle.
Using the principle of superposition again:
The intensity I is given by:
1. Standing Waves: Formed by z1 and z2.
- Intensity is zero at x=(2n+1)π2k.
2. Waves at 45 Degrees: Formed by z1 and z3.
- Intensity is zero at kx−ky=(2n+1)π.
Topper's Solved these Questions
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (NUMERICAL VALUE TYPE)
21 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
Similar Questions
The following equations represent progressive transverse waves
z1=Acos(ωt−kx)
z2=Acos(ωt+kx)
z3=Acos(ωt+ky)
z4=Acos(2ωt−2ky)
A stationary wave will be formed by superposing
View SolutionConsider the three waves z1,z2andz3 as
z1=Asin(kx−ωt)
z2=Asin(kx+ωt)
z3=Asin(ky−ωt)
Which of the following represents a standing wave?
View Solution
Knowledge Check
Three travelling waves are superimposed. The equations of the wave are
y!=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) and y3=4A0cos(kx−ωt)
find the value of ϕ(given 0≤ϕ≤π/2) if the phase difference between the resultant wave and first wave is π/4Aπ6Bπ3Cπ12DNone of these
Which two of the given transverse waves will give stationary wave when get superimposed?
z1=acos(kx−ωt) (A)
z2=acos(kx+ωt) (B)
z3=acos(ky−ωt) (C)
View SolutionWhich of the following equations can form stationary waves?
(i)y=Asin(ωt−kx) (ii) y=Acos(ωt−kx)
(iii) y=Asin(ωt+kx) (iv) y=Acos(ωt−kx) .
View SolutionWhich of the following functions represent SHM :-
(i) sin2ωt , (ii) sinωt+2cosωt , (iii) sinωt+cos2ωt
View SolutionThe equation y=Asin2(kx−ωt) represents a wave motion with
View SolutionIn a wave motion y=asin(kx−ωt), y can represent
View Solution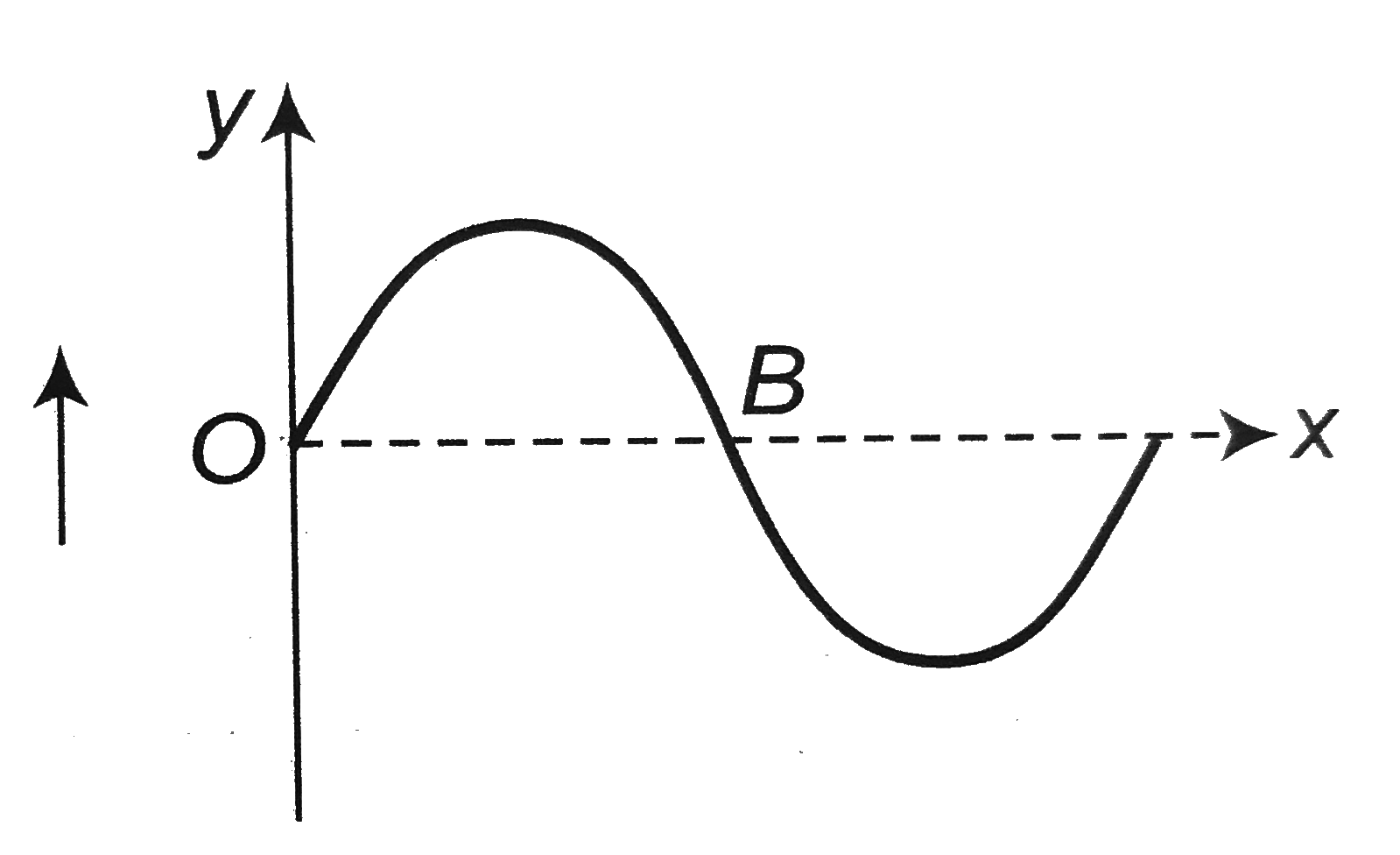
Figure below shows the wave y=Asin(ωt−kx) at any instant travelling in the +ve x-direction. What is the slope of the curve at B?
View SolutionAssertion: Two equations of wave are y1=Asin(ωt−kx)andy2Asin(kx−ωt). These two waves have a phase difference of π.
Reason: They are travelling in opposite directions.
View Solution
