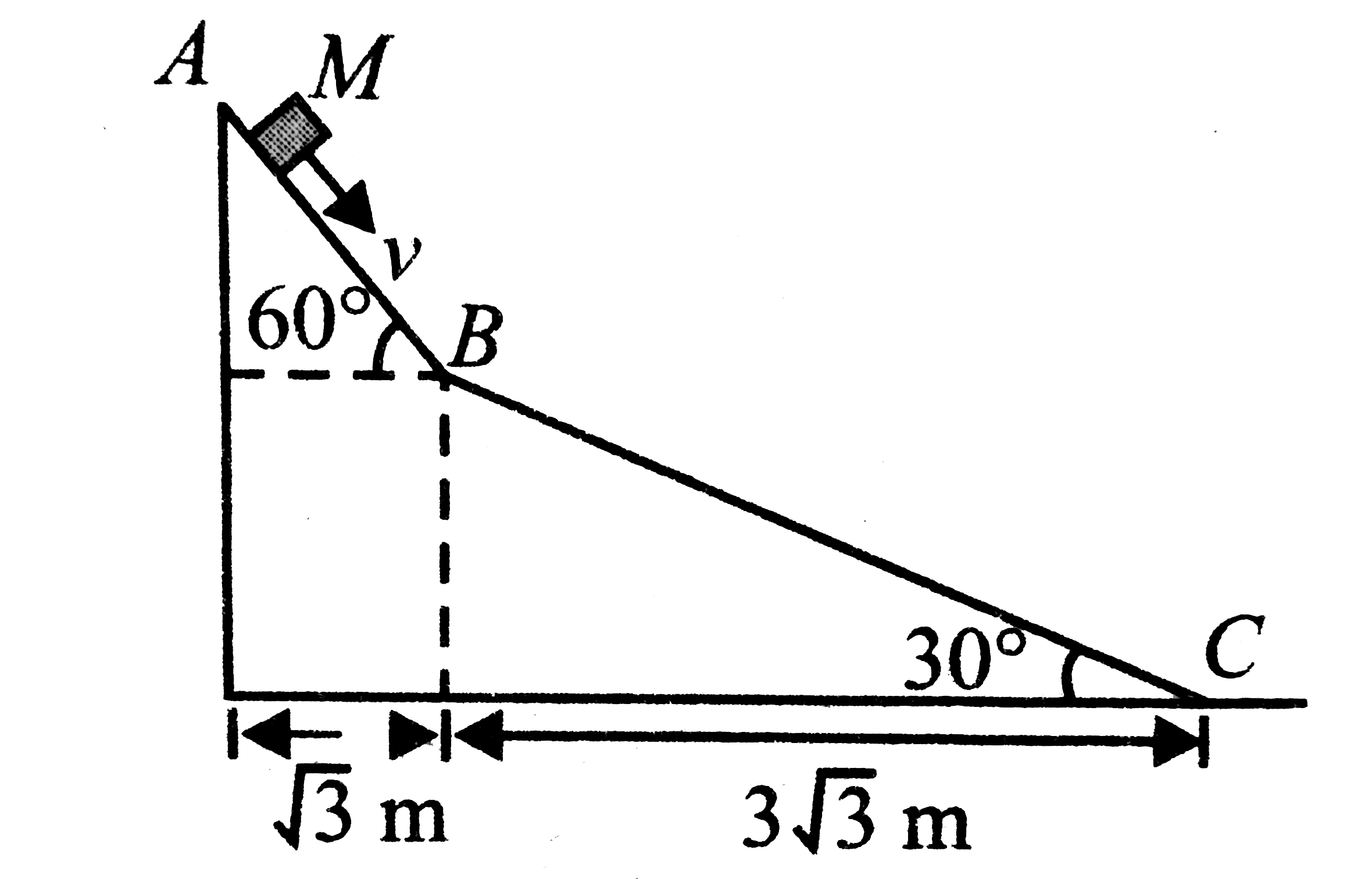
A small block of mass M move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from 60∘ to 30∘ at point B . The block is initally at rest at A Assume the collsion between the block and the incline are totally inclassic (g=10m/s2)
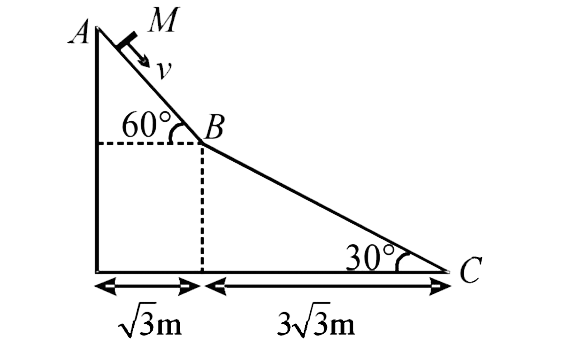
If collision between the block and the incline is completely elestic , then the vartical (apward) component of the of the block at point B immediatly after it stricess the scond indine is -
√30m/s
√15m/s
0
−√15m/s
The correct Answer is:C
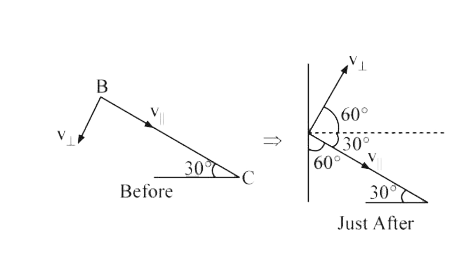
In elastic collision, component of v1 parallel to BC will remain unchanged, while component perpendicular to BC will remain unchanged in magnitude but its direction will be reversed.
v⊥=v1cos30∘=(√60)(√32)=√45m/s
v⊥=v1sin30∘=(√60)(12)=√15m/s
Now the vertical component of velocity of the block,
v'=v⊥cos30∘=v∣∣cos60∘ =(√15)(√32)−(√45)(12)=0
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - MATCH MATRIX TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE)80videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
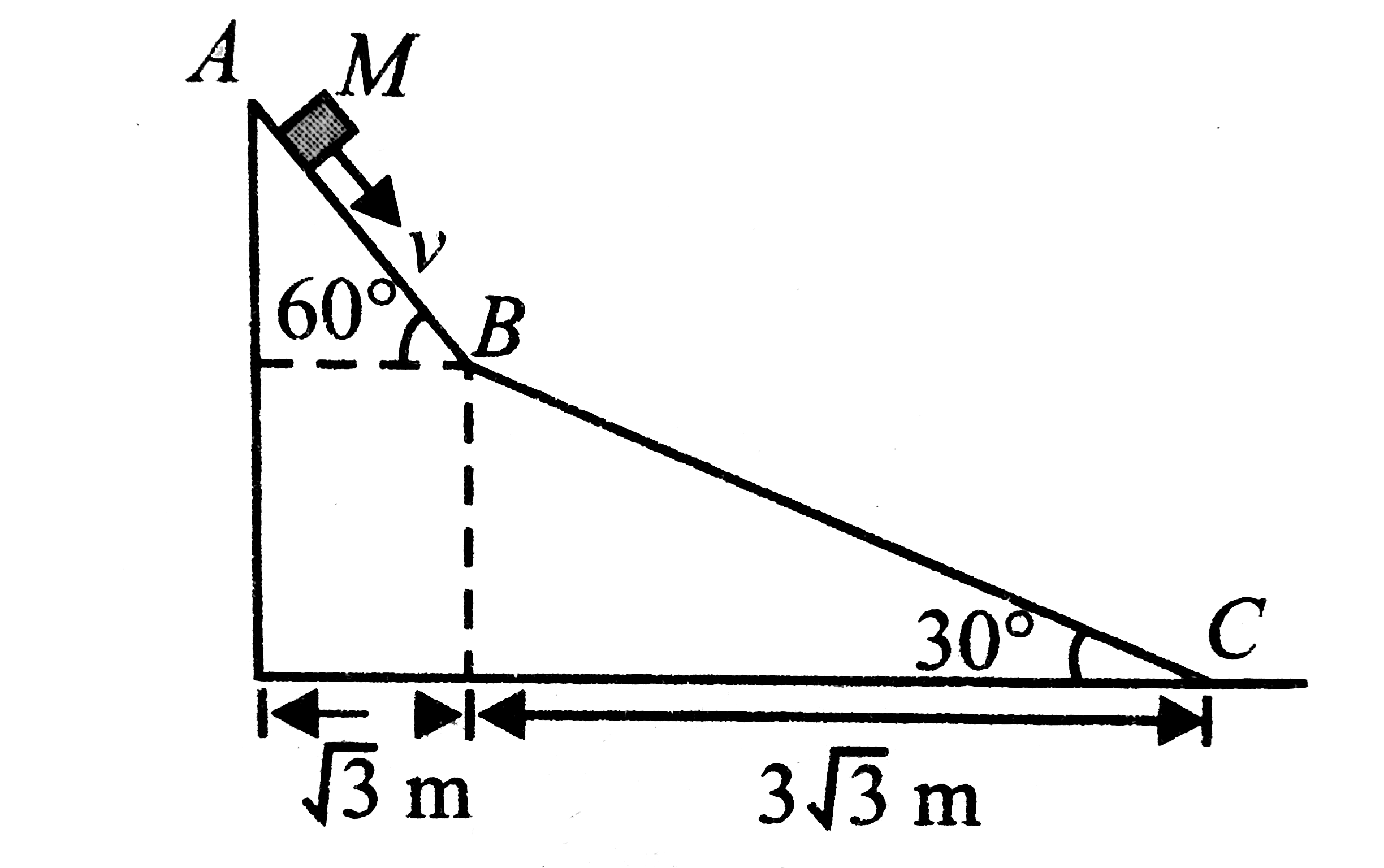
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
 View Solution
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
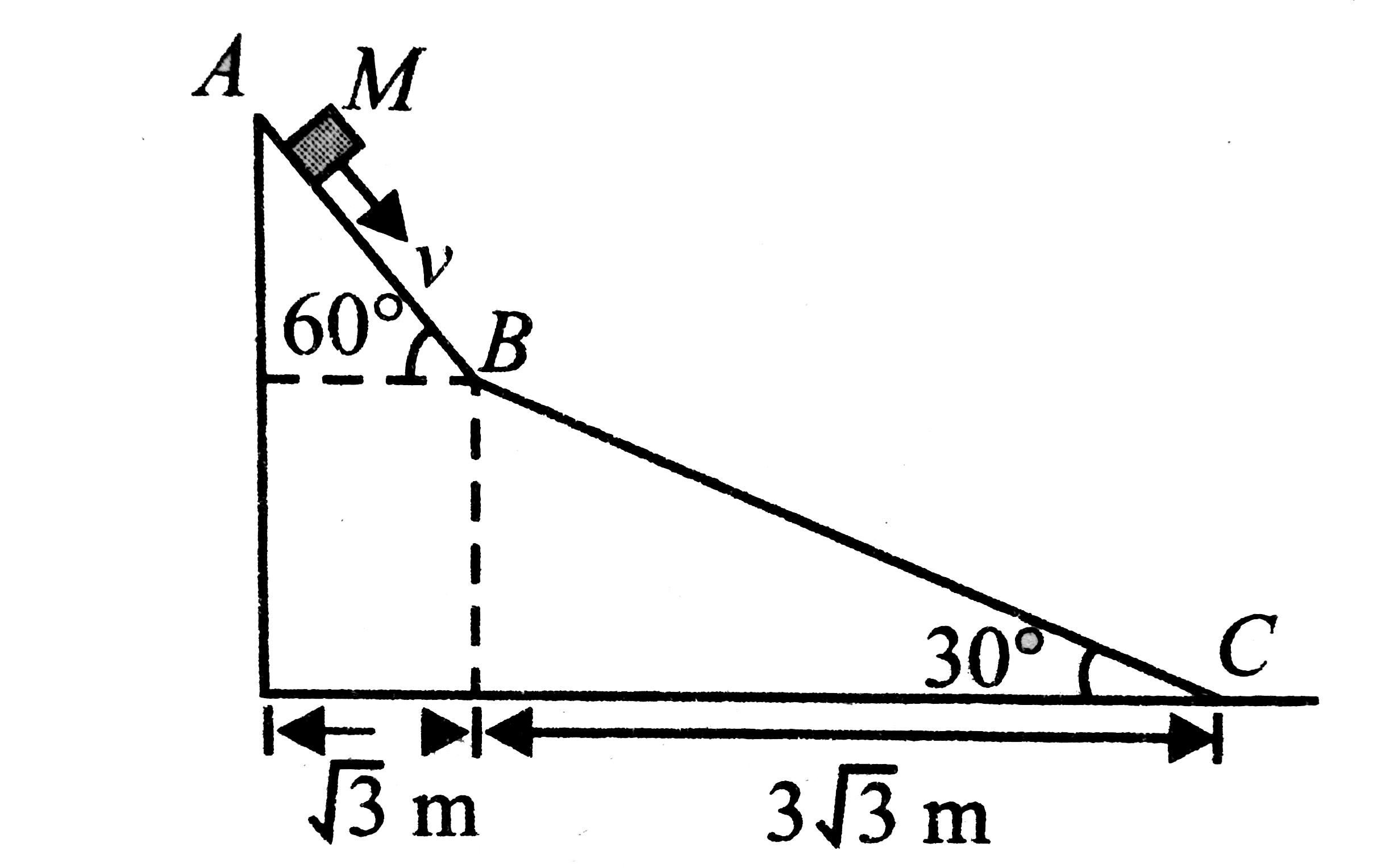
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point B immediately after it strikes the second incline is
 A√60 m/sB√45 m/sC√30 m/sD√15 m/s
A√60 m/sB√45 m/sC√30 m/sD√15 m/s - Question 2 - Select One
A small block of mass M moves on a friction-less surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is initially at rest at A.
If collision between the block and the incline is completely elastic, then the vertical (upward) component of the velocity of the blocks at point B, immediately after it strikes the second incline is
 A√30 m/sB√15 m/sC0D−√15 m/s
A√30 m/sB√15 m/sC0D−√15 m/s
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block
 View Solution
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass 3kg is at rest on a rough inclined plan as shown in the Figure. The magnitude of net force exerted by the surface on the block will be
 View Solution
View Solution

