A cylindrical tank whose cross-section area is 2000cm2 has a hole in its bottom 1cm2 in area.
(i) If the water is allowed to flow into the tank from a tube above it at the rate of 140 cm3/s, how high will the water in the tank rise ?
(ii) If the flow of water into the tank is stopped after the above height has been reached, how long will it take for tank to empty itself through the hole?
To solve the problem step by step, we will break it down into two parts as per the question.
Part (i): Finding the height of water in the tank
1. Given Data:
- Cross-sectional area of the tank, A=2000cm2
- Area of the hole, a=1cm2
- Rate of water flow into the tank, Q=140cm3/s
2. Calculate the velocity of water entering the tank:
- The volume flow rate Q is related to the height H of the water in the tank by the equation:
Q=A⋅dHdt
- Rearranging gives:
dHdt=QA
3. Calculate the height of water when it reaches equilibrium:
- At equilibrium, the rate of water entering the tank equals the rate of water flowing out through the hole.
- The velocity of water flowing out through the hole can be calculated using Torricelli's theorem:
v=√2gH
- The volume flow rate out of the hole is:
Qout=a⋅v=a⋅√2gH
- Setting the two flow rates equal gives:
Q=a⋅√2gH
- Substituting the known values:
140=1⋅√2⋅980⋅H
- Squaring both sides:
19600=2⋅980⋅H
- Solving for H:
H=196001960=10cm
Part (ii): Finding the time to empty the tank
1. Using the height found in part (i):
- We have H=10cm.
2. Setting up the equation for the time to empty:
- The volume of water in the tank is given by:
V=A⋅H=2000⋅10=20000cm3
3. Using the flow rate out of the hole:
- The flow rate out of the hole when the height is H is:
Qout=a⋅√2gH=1⋅√2⋅980⋅10=√19600=140cm3/s
4. Calculating the time to empty the tank:
- The time t to empty the tank is given by:
t=VQout=20000140≈142.86s
5. Converting seconds to minutes:
- t≈142.86s≈2minutes22.86seconds
Final Answers:
- (i) The height of water in the tank will rise to 10 cm.
- (ii) It will take approximately 2 minutes and 23 seconds for the tank to empty.
- Cross-sectional area of the tank, A=2000cm2
- Area of the hole, a=1cm2
- Rate of water flow into the tank, Q=140cm3/s
- The volume flow rate Q is related to the height H of the water in the tank by the equation:
Q=A⋅dHdt
- Rearranging gives:
dHdt=QA
- At equilibrium, the rate of water entering the tank equals the rate of water flowing out through the hole.
- The velocity of water flowing out through the hole can be calculated using Torricelli's theorem:
v=√2gH
- The volume flow rate out of the hole is:
Qout=a⋅v=a⋅√2gH
- Setting the two flow rates equal gives:
Q=a⋅√2gH
- Substituting the known values:
140=1⋅√2⋅980⋅H
- Squaring both sides:
19600=2⋅980⋅H
- Solving for H:
H=196001960=10cm
- We have H=10cm.
- The volume of water in the tank is given by:
V=A⋅H=2000⋅10=20000cm3
- The flow rate out of the hole when the height is H is:
Qout=a⋅√2gH=1⋅√2⋅980⋅10=√19600=140cm3/s
- The time t to empty the tank is given by:
t=VQout=20000140≈142.86s
- t≈142.86s≈2minutes22.86seconds
- (i) The height of water in the tank will rise to 10 cm.
- (ii) It will take approximately 2 minutes and 23 seconds for the tank to empty.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -190videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -250videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - I )7videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
The liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
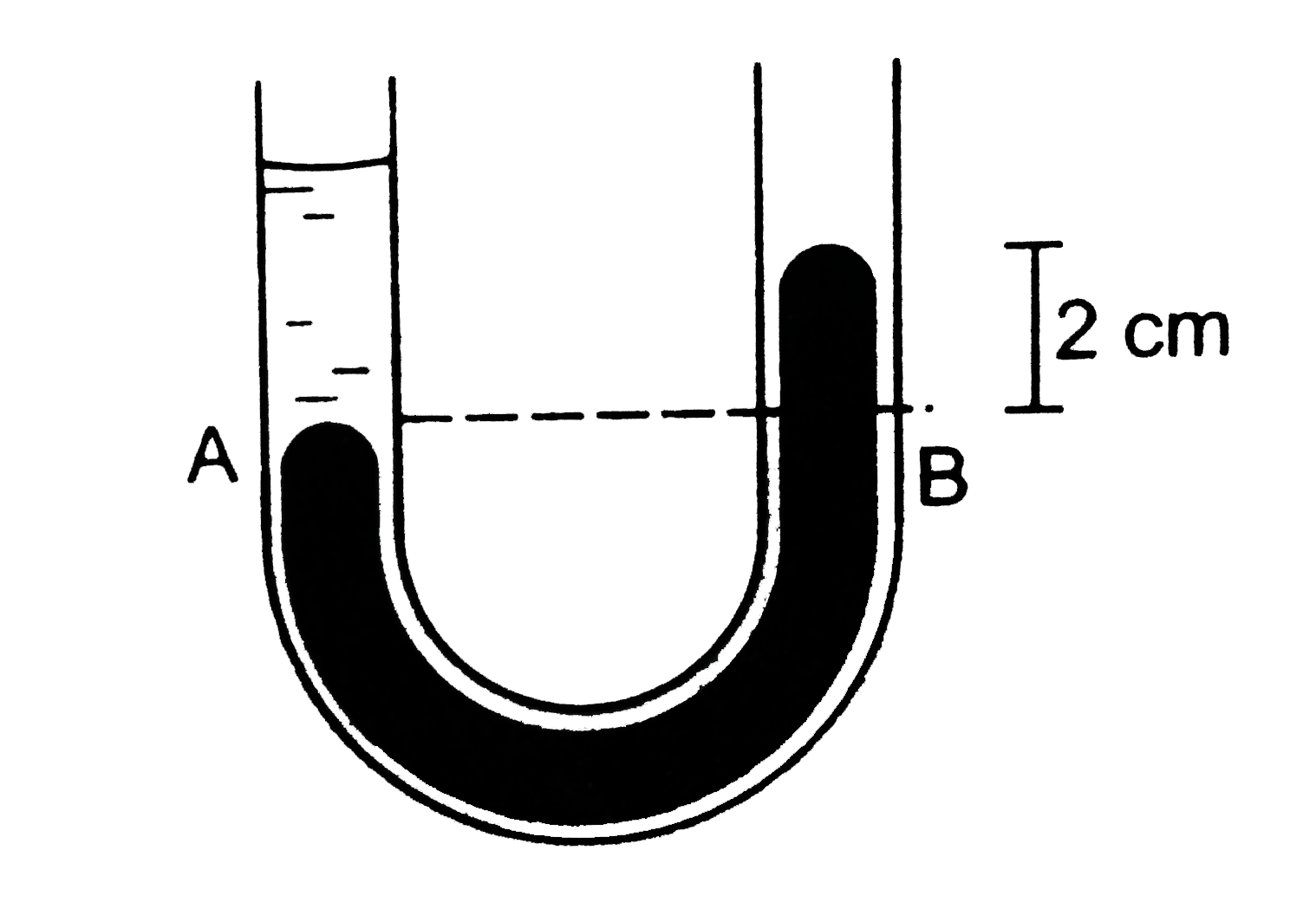 ,06:12View Solution
,06:12View SolutionIn a U-tube, two immiscible liquids of density ρ1andρ2 are arranged as shown in figure. The right part of the tube is closed at the top and some air is entrapped above liquid of density ρ2. The gauge pressure of this air is :
 03:16View Solution
03:16View SolutionState Archimedes, principle.
03:54View SolutionCoefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
03:18View SolutionA circular loop of radius R carrying a current I is placed in a uniform magnetic field B perpendicular to the loop. The force on the loop is
05:15View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
View SolutionA cylindrical tank has a hole of 1cm^(2) in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm^(3)//sec , then the maximum height up to which water can rise in the tank is
12:07View SolutionA cylindrical tank has a holes of 3cm2 in its bottom. If the water is allowed to flow into the tank form a tube above it at the rate of 80cm3/sec. Then the maximum height up to which water can rise in the tank is
View SolutionThe level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
View SolutionA cylindrical tank has a hole of 1 cm in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm/sec . then the maximum height up to which water can rise in the tank is
02:59View SolutionA cylinderal tank has a hole of 1.6cm2 in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 80cm3/s, then the maximum height up to which water can water can rise in the tank is
08:42View SolutionA cylindrical tank whose cross-section area is 2000 cm^2 has a hole in its bottom 1 cm ^2 in area. (i) If the water is allowed to flow into the tank from a tube above it at the rate of 140 cm ^3//s , how high will the water in the tank rise ? (ii) If the flow of water into the tank is stopped after the above height has been reached, how long will it take for tank to empty itself through the hole?
01:53View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by a tube of equal cross-sectional area A ejecting water at the speed upsilon .
03:59View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by as tube of equal cross sectional area A ejecting water at the speed v.
03:21View SolutionA tank is filled to a height of 5 m. 10 cm in the bottom of the tank. ""^(2) Is a hole in the area of. Then the water flow rate is
04:27View Solution

