According to Biot-Savart’s law, magnetic field due to a straight current carrying wire at a point, at a distance r from it, is given by B=μ0I4πr(sinθ1+sinθ2). The direction of magnetic field being perpendicular to the plane containing the wire and that point.

In the figure shown, a closed loop AOCBA in which current I is flowing as shown. Given OA = OB = OC = a. Find the magnetic field at point B due to the loop.

−μ0I4πa(ˆi+ˆk)
−μ0I4πa(ˆj+ˆk)
−μ0I2πa(ˆj+ˆk)
−μ0I2√2πa(ˆj+ˆk)
The correct Answer is:C
At O : Magnetic field due to AO and OC will be zero.
Due to CB:r=acos45∘=a√2
→BCB=μ04πIr[sin45∘+sin45∘](−ˆk)=−μ0I2πaˆk
similarly, →BBA=−μ02πIaˆj∴→Bnet=→BCB+→BBA=−μ02πIa(ˆj+ˆk)
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
According to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
B=μ0I4πr(sinϕ1+sinϕ2)
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

Figure, shows a closed loop AOCBA in which current I is flowing as shown. Given OA=OB=OC=a. Find the magnetic field at point B due to this loop.

View SolutionAccording to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
B=μ0I4πr(sinϕ1+sinϕ2)
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

Find magnetic field at point O in Fig.
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

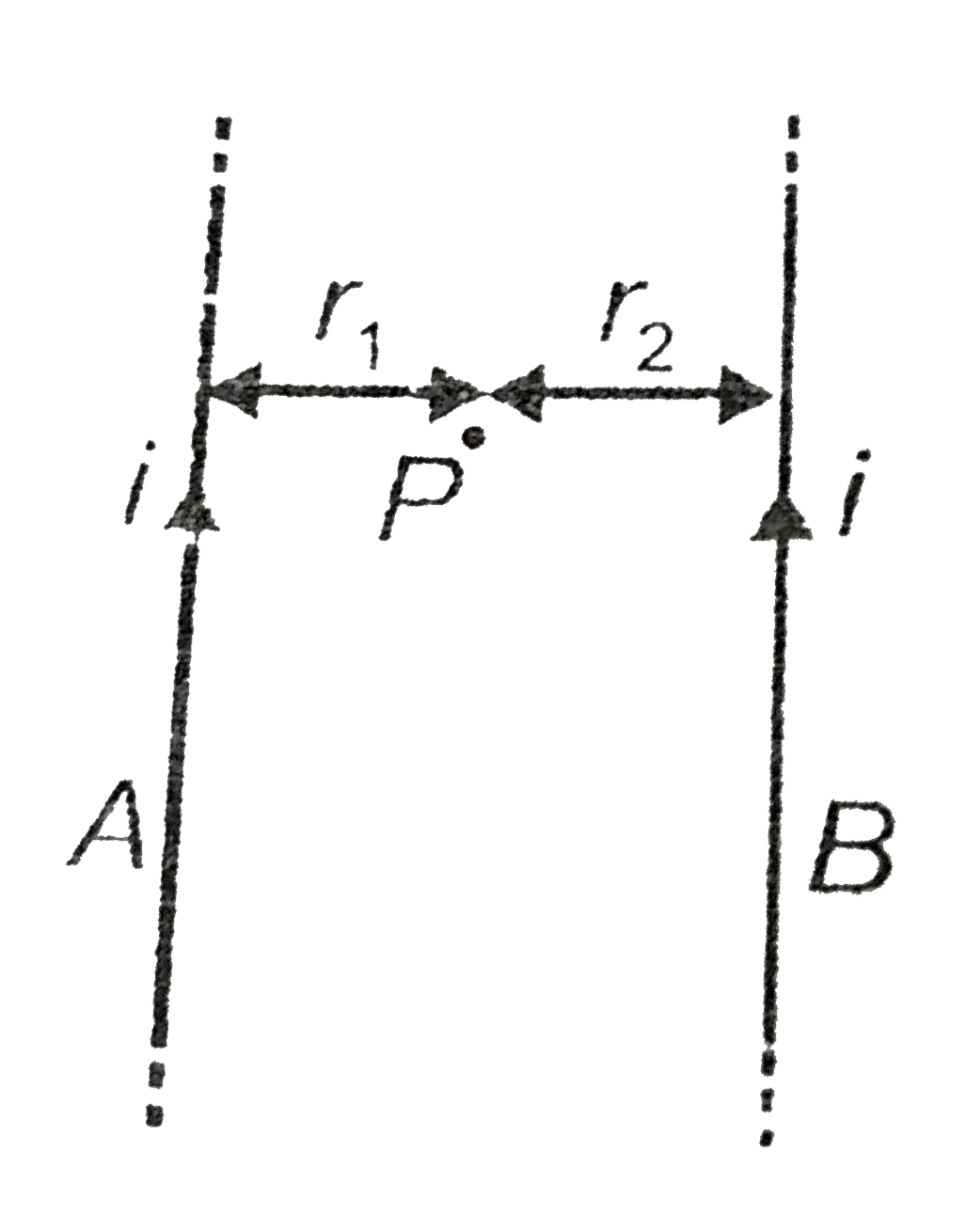
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

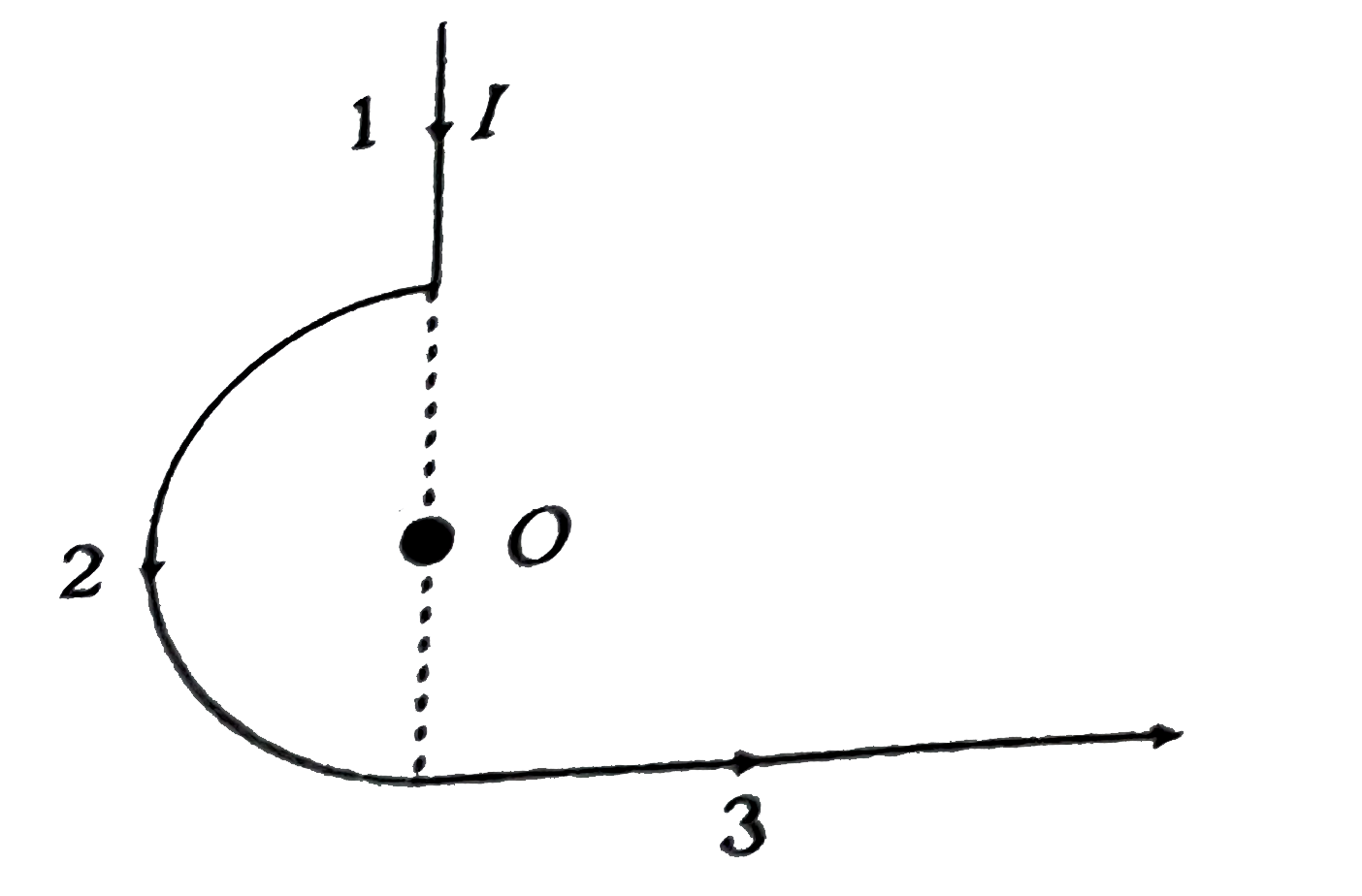
View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
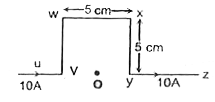
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View Solution
