A long, hollow insulating cylinder of radius R and negligible thickness has a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω. Choose the correct option(s):
The charge crossing an imaginary line of length L on the surface of the cylinder, parallel to its axis, per unit time, is ωσRL.
The magnetic moment of a length L of the cylinder is πωσR3L
The magnetic field intensity at a point on the axis of the cylinder, inside the cylinder, is μ0ωσR2
If the direction of rotation of the cylinder is reversed, the magnetic field at a point on the axis of the cylinder will also reverse direction
The correct Answer is:A, B, D
Consider a length L of the cylinder. All the charge on this length will pass through the given line of length L parallel to the axis of the cylinder in the time it takes the cylinder to complete one full rotation.
Total charge on this length L of the cylinder,
Q=σ(2πR)L
So, change crossing per unit time =Q(2πω)=ωσRL
This is like an equivalen current Ieq carried by the this length L of the cylinder.
so its magnetic moment m=Ieq(πR2)=πomegσR3L
Now, this rotating cylinder is exactly equivalent to a long solenoid carrying a current.
Magnetic field at a point on the axis of a solenoid with N turns per unit length carrying a current I,
B=μ0NI
This field can be looked at as B=μ0(NI) , where NI is the “total current” carried by a unit length of the solenoid. In other words, it is the current per unit length. The current per unit length carried by the rotating cylinder is ωσR. So, field due at a point on the axis of the cylinder B=μ0(ωσR)
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
A thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
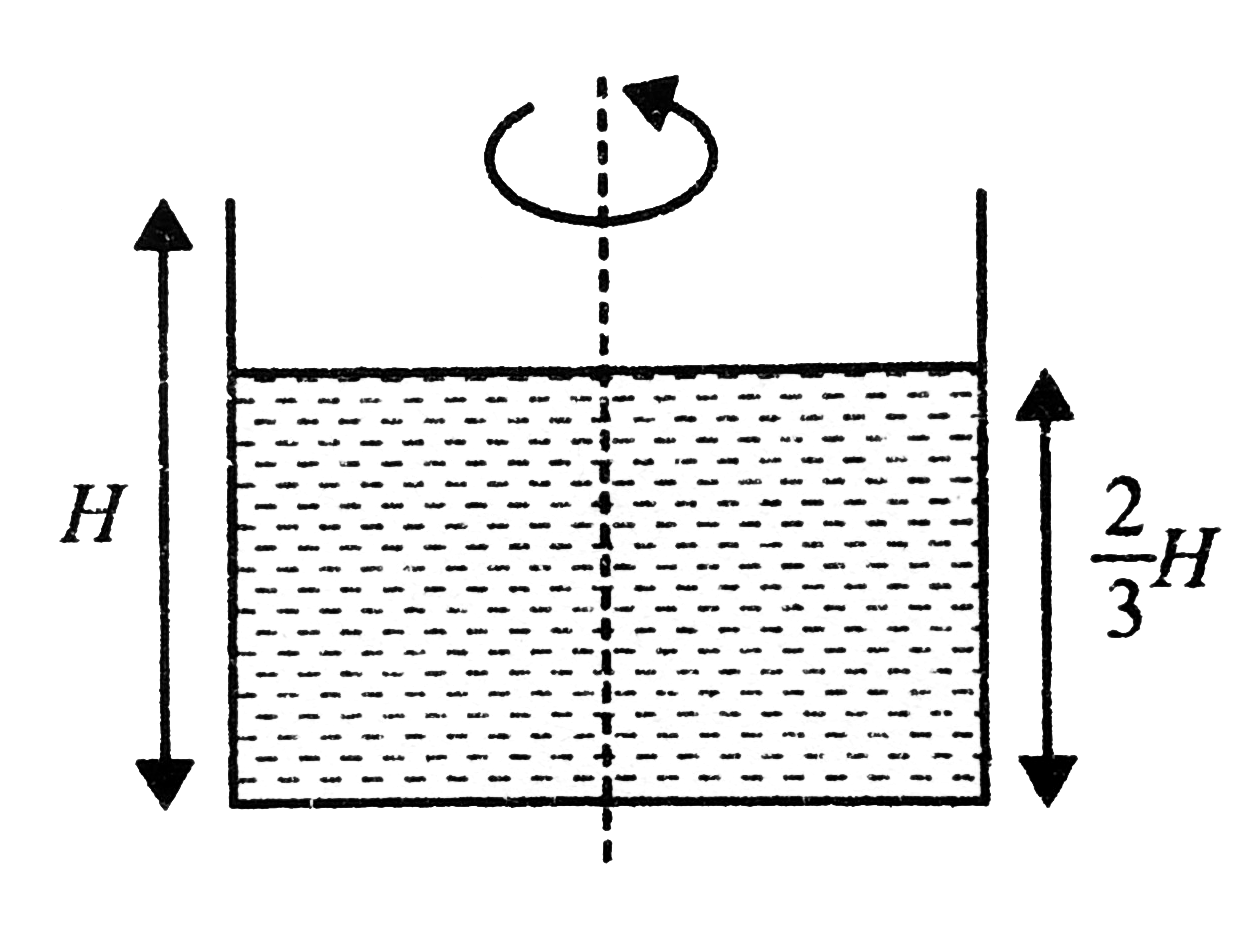
A circular cylinder of radius R and height H is filled with water to a height (2/3)H. It starts rotating about its axis with constantly increasing angular speed. Choose the correct alternatives.
View SolutionA thin circular disk of radius R is uniformly charged with density σ>0 per unit area.The disk rotates about its axis with a uniform angular speed ω.The magnetic moment of the disk is :
View SolutionA particle is revolving in a circle of radius r and centre at 'O' with uniform angular velocity ω. Choose the correct option(s) :

View SolutionA very long metallic hollow pipe of length l and radius r(<<l) is carrying charge Q , uniformly distributed upon it . The pipe is rotated about its axis with constant angular speed ω . The energy stored in the pipe of length l100 is
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionChoose the correct option:
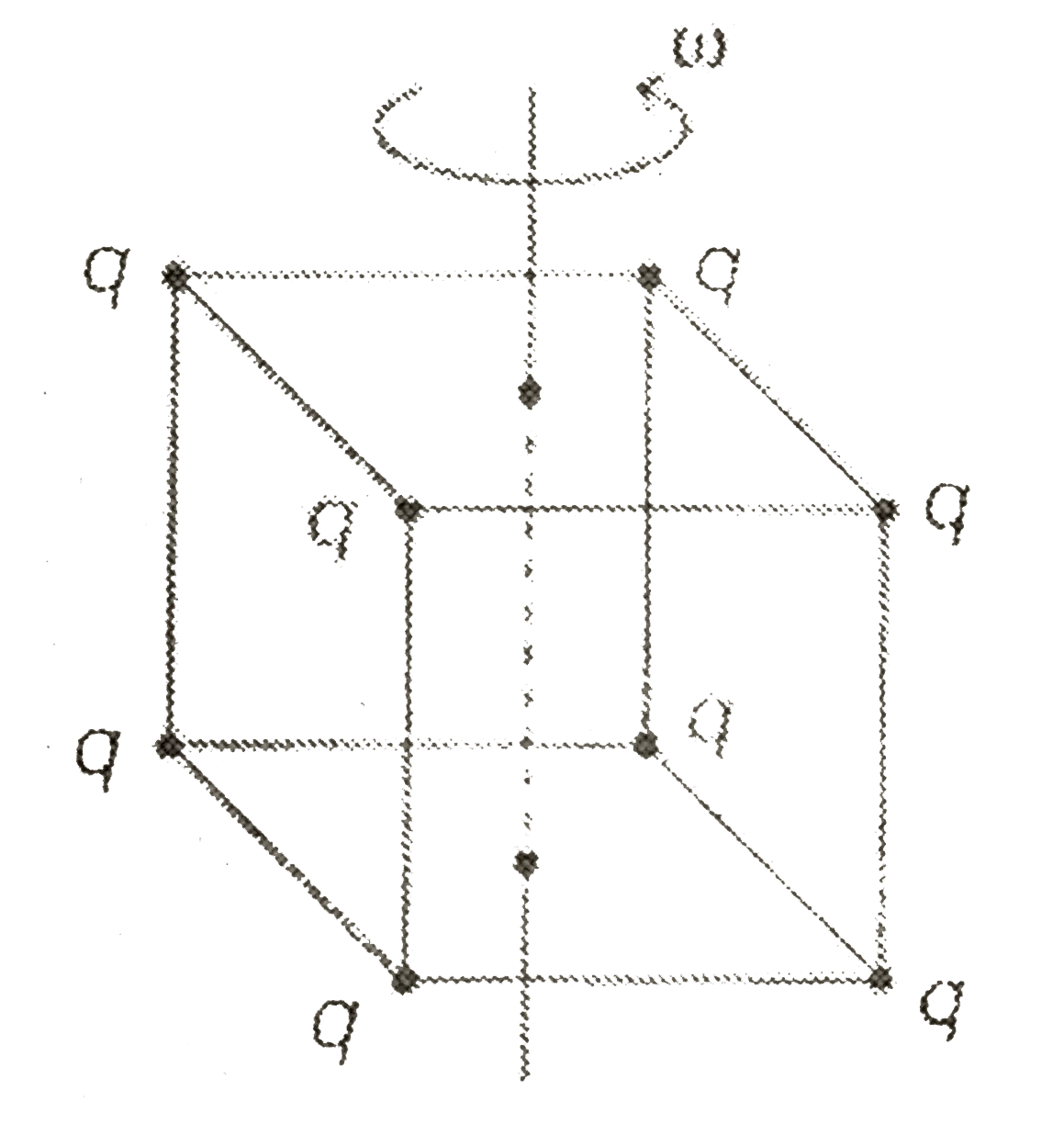
Consider a cube of side 'a' as shown. Eight point charges are placed at the corners. The cube is rotated about the central axis with constant angular velocity ω :
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution
