A uniform magnetic field of intensity B exists only inside a rectangular region MNOP with dimensions as shown. The direction of the field is out of the paper perpendicular to the paper. An electron of mass m and carrying charge e enters the region with velocity u perpendicular to MP. Pick the correct choice(s):
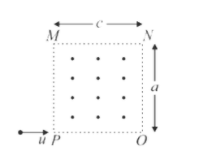
The electron leaves the region from side NO if u>eBcm
The electron leaves the region from side MN if eBCm>u>eBa2m and a<2c
The electron leaves the region from side PM if u<eBa2m and u<eBcm
The electron gets trapped inside the region if u<eBa2m and a<2c
The correct Answer is:A, B, C
Radius of circular path of electron r=mueB
(i) If r>c, electron leaves from side NO
⇒mueB>C⇒u>eBcm
(ii) If r<c but 2r>a, electron leaves from side MN
⇒a2<mueB<c⇒eBa2m<u<eBcm
and Also a<2c
(iii) If r<c but 2r<a, electron leaves from side MP
⇒mueB<c and mueB<a2
⇒u<eBcm and t–eBa2m
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
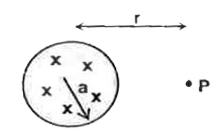
A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View Solution
Knowledge Check
A uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
 Ais zeroBproportional to rCproportional to 1/rDproportional 1/r2
Ais zeroBproportional to rCproportional to 1/rDproportional 1/r2A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 Ais zeroBdecreases as 1rCIncreases as rDdecreases as 1r2
Ais zeroBdecreases as 1rCIncreases as rDdecreases as 1r2A uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.
 Ais zeroBdecreases as 1rCincreases as rDdecreases as 1r2
Ais zeroBdecreases as 1rCincreases as rDdecreases as 1r2
An electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionAn electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View Solution
