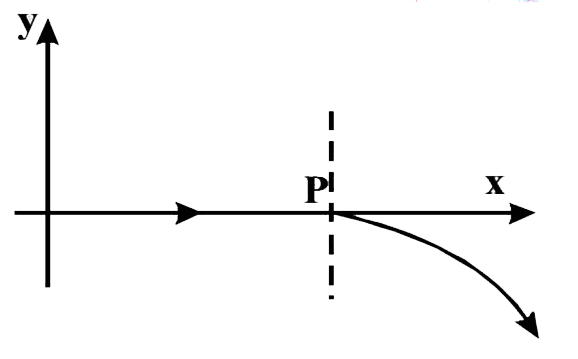
For a positively charged particle moving in a $x - y$ plane initially along the $x - a ξ s$ , there is a sudden change in its path due to the presence of electric and//or magnetic fields beyond $p$ . The curved path is shown in the $x - y$ plane and is found to be non - circular. Which one of the following combinations is possible ?

A

$E = 0, B = b ˆ j + c ˆ k$

B

$E = a ˆ, B = c ˆ k + a ˆ i$

C

$E = 0, B = c ˆ j + b ˆ k$

D

$E = a ˆ i, B = c ˆ k + b ˆ j$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Electric field can deviate the path of the particle in the shown direction only when it is along negative y-direction. In the given options E is either zero or along x-direction. Hence, it is the magnetic field which is really responsible for its curved path. Options (A) and (C) cannot be accepted as the path will be circular in that case. Option (D) is wrong because in that case component of net force on the particle also comes in direction which is not acceptable as the particle is moving in x-y plane. Only in option (B) the particle can move in x-y plane. In option (D) $F_{net} = q E + q (v + B)$ initial is along x-direction. So let $v = v ˆ i$
$∴ F_{net} = q a ˆ i + q [(v ˆ i) \times (c ˆ k + b j)] = q a ˆ i - q v c ˆ j + q v b ˆ k$ . In the onption b $F_{net} = q (a i) + q [(v ˆ i) \times (ˆ k + a ˆ i)] = q a ˆ i + q v c ˆ j$

|

Updated on:21/07/2023

Class 12 PHYSICS MAGNETIC EFFECTS OF CURRENT

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-MAGNETIC EFFECTS OF CURRENT -JEE Advanced (Archive)

Home
Ask Doubt
Profile