The given figure shown a change of state A to state C by two paths ABC and AC for an ideal gas. Calculate the :
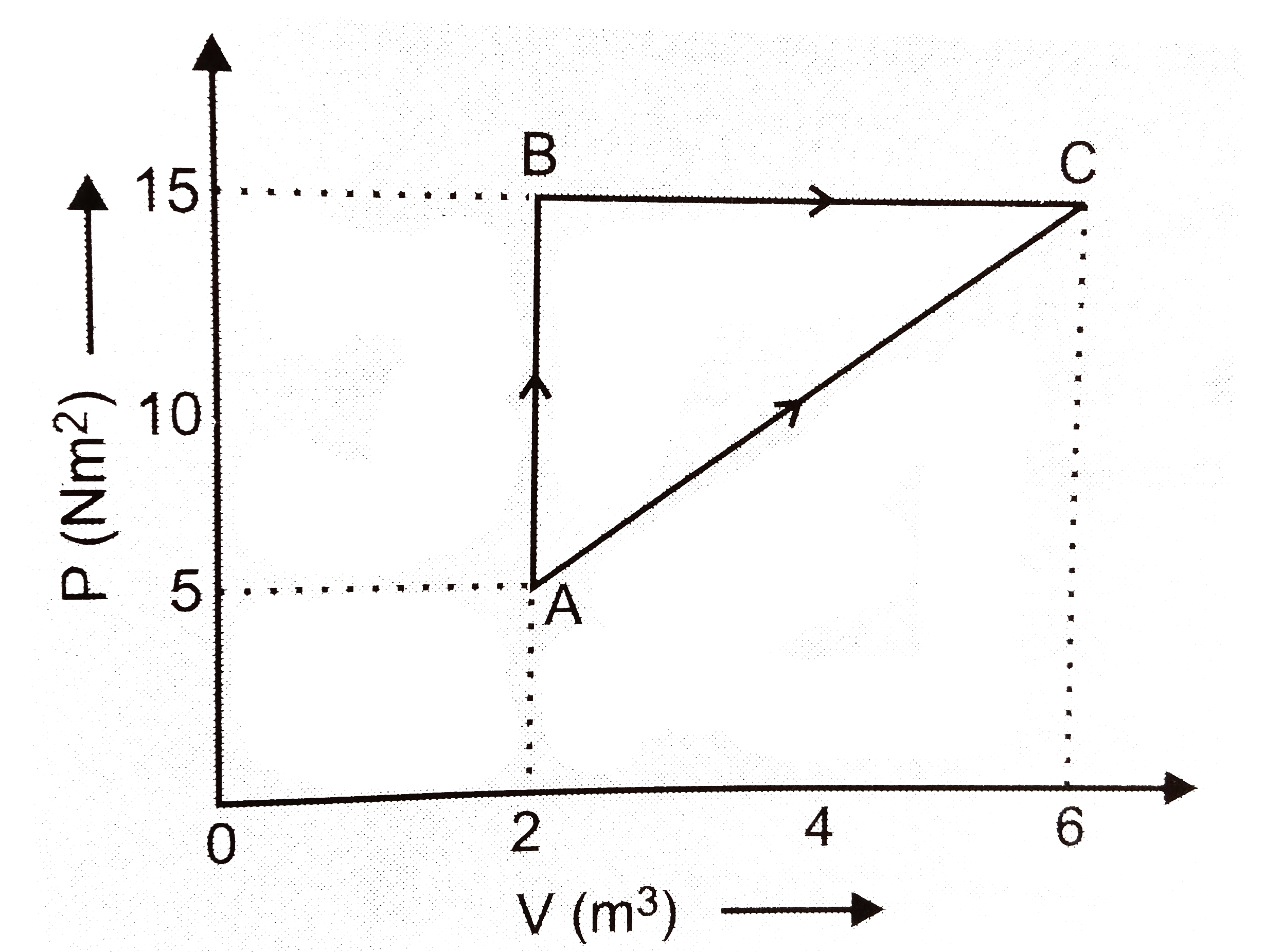
(a) Path along which work done is least.
(b) Internal energy at C if the internal energy of gas at A is 10J and amount of heat supplied to change its state to C through the path AC is 200J.
(c) Amount of heat supplied ot the gas to go from A to B, if internal energy of gas at state B is 10J.
We know,
Path CA - Isothermal compression
Path AB - Isobaric expansion
Path BC - Isochoric change
Let V1 and Vf are initial volume and final volume at respective points.
For temperature T1 (For C):
PV=nRT1
2×10=1×0.0821×T1
T1=243.60 K
For temperature T2 (For C and B)
P1V1T1=P2V2T2
=2×10T1=20×10T2
∴T2T1=10∴T2=243.60×10=24360 K
Path CA : w=+2.303nRT1logV1Vf=2.303×1×2×243.6log101=+1122.02 cal
ΔE=0 for isothermal compression, Also q=Q
Path AB W=−P(Vt−Vi)
=20×(10−1)=−180 litre atm
=−180×20.0821=−4384.9 cal
Path BC, W=−P(Vt−Vi)=0(∴Vt−Vi=0) since volume is constant
For monoatomic gas heat charge at constant volume =qv=ΔE
Thus for path BC.
qv=Cv×n×ΔT=ΔE
∴qv=32R×1×(2436−243.6)=32×2×1×2192A=6577.2cal
Since process involves cooling
qv=ΔE=−6577.2 cal
Also in path AB, the internal energy in state A and state C is same. Thus during path AB, an increase in internal energy equivalent of change in internal energy during path BC should take place. Thus, ΔE for path AB = +6572.2 cal Now q for path AB=ΔE−WAB=6577.2+4384.9=10962.1 cal
Cycle ΔE=0,
q=−W=−[Wpath CA+Wpath AB+Wpath BC)
=−[+1122.02+(−4384.9)+0]
q=−W=+3262.88 cal
Topper's Solved these Questions
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:LEVEL-1
Explore 75 Videos
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:LEVEL-2
Explore 50 Videos
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:LEVEL-0 (SHORT ANSWER TYPE-II (3 MAKRS))
Explore 6 Videos
- THERMOCHEMISTRYBook:VMC MODULES ENGLISHChapter:THERMOCHEMISTRYExercise:JEE ADVANCED (ARCHIVE)
Explore 31 Videos
- THERMODYNAMICS & THERMOCHEMISTRYBook:VMC MODULES ENGLISHChapter:THERMODYNAMICS & THERMOCHEMISTRYExercise:Impeccable
Explore 48 Videos
Similar Questions
The relationship between enthalpy and internal energy change is
View SolutionIn the given figure, an ideal gas changes it state from A to state C by two paths ABC and AC.
(i) Find the path along which work done is the least.
(ii) The internal energy of the gas at A to 10J and the amount of heat supplied to change its state to C through the path AC is 200J. Calculate the internal energy at C.
(iii) The internal energy of the gas at state B is 30J. Find the amount of heat supplied to the gas to go from A→B.

View SolutionIn the given figure an ideal gas changes its state from A to state C by two paths ABC and AC.
_E01_269_Q01.png)
(i) Find the path along which work done is the least.
(ii) The internal energy of gas at A and B is 10J and 20 J respectively amount of heat supplied to change its state to C through the path AC is 200J. Calculate the internal energy at C.
(iii) How much is the heat involved in the process ABC and ADC?
View SolutionIn the given figure, an ideal gas changes its state from state state C by two paths ABC and AC.
_E01_269_Q01.png)
The internal energy of gas at A is 10 J and the amount of heat supplied to change its state to C through path AC is 200 J.Calculate the internal energy of gas at C
View SolutionIn the given graph, an ideal gas changes its state from A to C by two paths ABC and AC.
(a) Find the path along which work done is less.
(b) The internal energy of gas at A is 10J and the amount of heat supplied in path AC is 200J. Calculate the internal energy of gas at C.
(c) The internal energy of gas at state B is 20J. Find the amount of heat supplied to the gas to go from A to B.
View SolutionFigure shows an ideal gas changing its state A to state C by two different path ABC and AC. The internal energy of the gas at A is 10J and the amount of heat supplied to change its state to C through the path AC is 200J. Find the internal energy at C.
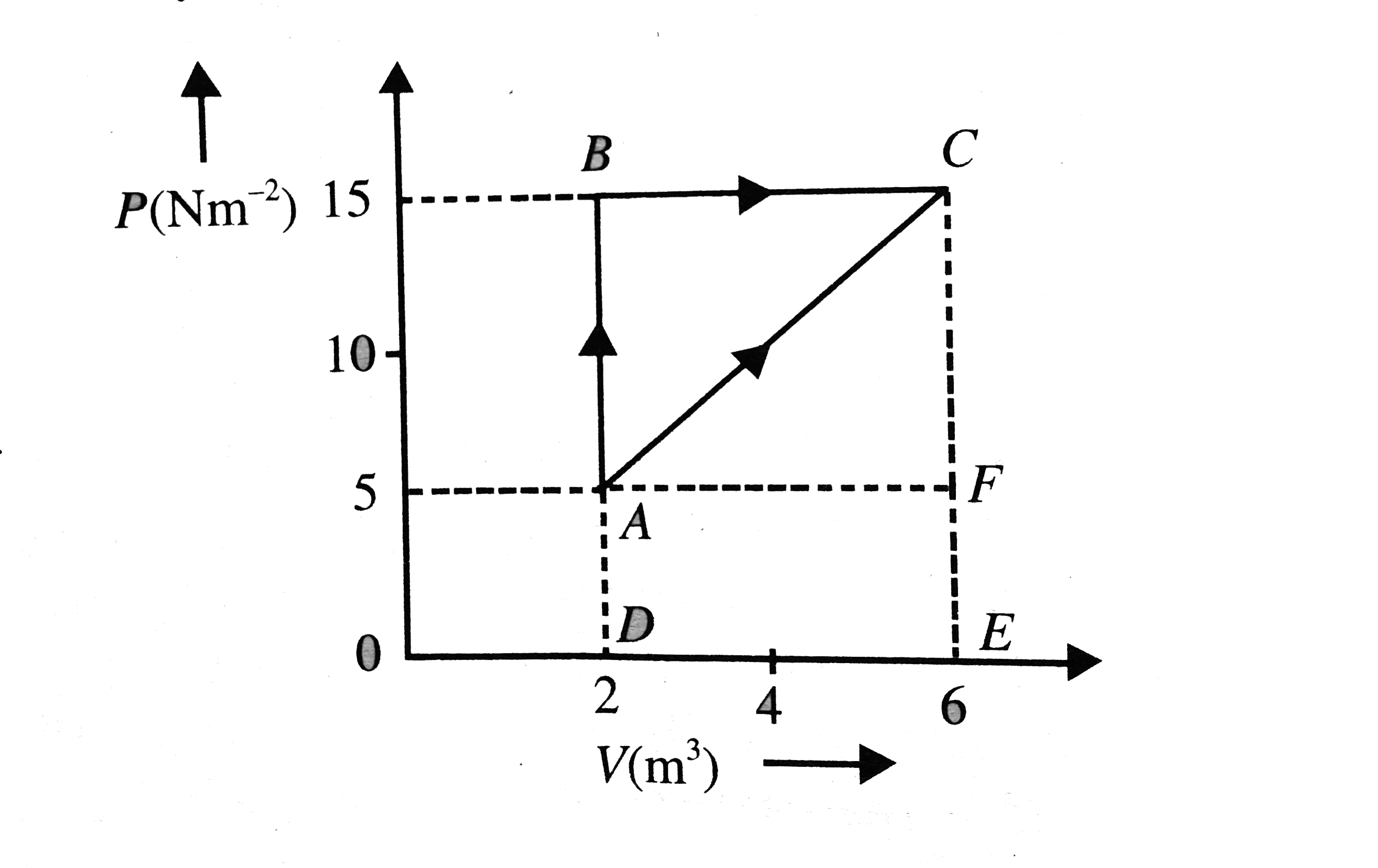
View SolutionIn the given figure, an ideal gas changes its state from A to state C by two paths ABC and AC.
_E01_269_Q01.png)
Along which path the work done by the gas is least.
View SolutionIn the given an ideal gas can change its state from A to C by two paths ABC or AC. Then
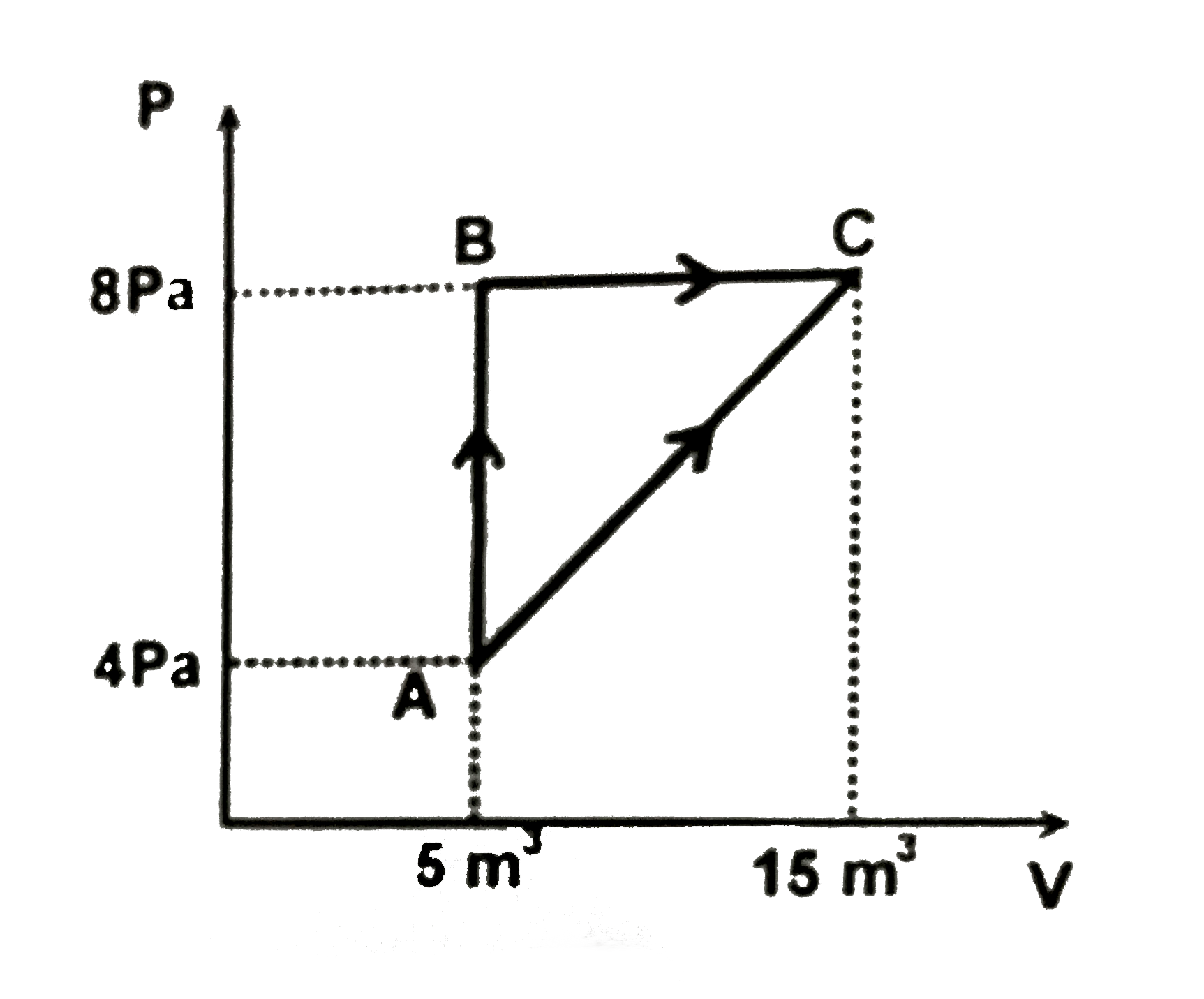
View Solutioncalculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
View SolutionIn the given figure, an ideal gas changes its state from A to C by four paths. The path for which work done is least, is
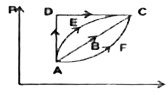
View Solution