130 g of Zn is dissolved in dilute sulphuric acid in an open beaker . Find the work done in the process assuming isothermal operation at 300K.
−1200 cal
−1800 cal
+1800 cal
none
The correct Answer is:A
To solve the problem of finding the work done when 130 g of zinc is dissolved in dilute sulfuric acid at 300 K, we can follow these steps:
Step 1: Write the Reaction Equation
The reaction of zinc with dilute sulfuric acid can be represented as:
Zn (s)+H2SO4(aq)→ZnSO4(aq)+H2(g)
Step 2: Calculate the Number of Moles of Zinc
To find the number of moles of zinc (Zn), we use the formula:
n=massmolar mass
Given:
- Mass of Zn = 130 g
- Molar mass of Zn = 65.38 g/mol
Calculating the number of moles:
n=130g65.38g/mol≈1.99moles
This can be approximated to 2 moles.
Step 3: Determine the Change in Moles of Gas (ΔNg)
In the reaction, 1 mole of zinc produces 1 mole of hydrogen gas (H₂). Therefore, the change in moles of gas (ΔNg) is:
ΔNg=moles of products−moles of reactants
ΔNg=1(from H2)−0(from Zn)=1
Step 4: Use the Formula for Work Done
The work done (W) in an isothermal process can be calculated using the formula:
W=−ΔNg⋅R⋅T
Where:
- R = 2 cal/K·mol (universal gas constant)
- T = 300 K
Substituting the values:
W=−1mol⋅2cal/K⋅mol⋅300K
W=−600cal
Step 5: Final Result
The work done in the process is:
W=−600cal
The reaction of zinc with dilute sulfuric acid can be represented as:
Zn (s)+H2SO4(aq)→ZnSO4(aq)+H2(g)
To find the number of moles of zinc (Zn), we use the formula:
n=massmolar mass
- Mass of Zn = 130 g
- Molar mass of Zn = 65.38 g/mol
n=130g65.38g/mol≈1.99moles
This can be approximated to 2 moles.
In the reaction, 1 mole of zinc produces 1 mole of hydrogen gas (H₂). Therefore, the change in moles of gas (ΔNg) is:
ΔNg=moles of products−moles of reactants
ΔNg=1(from H2)−0(from Zn)=1
The work done (W) in an isothermal process can be calculated using the formula:
W=−ΔNg⋅R⋅T
- R = 2 cal/K·mol (universal gas constant)
- T = 300 K
W=−1mol⋅2cal/K⋅mol⋅300K
W=−600cal
The work done in the process is:
W=−600cal
Topper's Solved these Questions
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-2
50 Videos
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-2 (NUMERICAL VALUE TYPE)
15 Videos
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-0 (LONG ANSWER TYPE (5 MARKS))
6 Videos
- THERMOCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - THERMOCHEMISTRYEXERCISE - JEE ADVANCED (ARCHIVE)
31 Videos
- THERMODYNAMICS & THERMOCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICS & THERMOCHEMISTRYEXERCISE - Impeccable
48 Videos
Similar Questions
One mole of a perfect gas, initally at a pressure and temperature of 105N/m2 and 300 K, respectively, expands isothermally unitl its volume is doubled and then adiabatically until its volume is again doubled. Find final pressure and temperature of the gas Find the total work done during the isothermal and adiabatic processes. Given γ=1.4. Also draw the P-V diagram for the process.

View SolutionWhen dissolved in dilute sulphuric acid, 0.275 g of a metal evolved 119.7 mL of hydrogen at 20°C and 763 mm pressure. What is the equivalent mass of the metal ?
View SolutionOne mole of solid Zn is placed in excess of dilute H2SO4 at 27∘C in a cylinder fitted with a piston . Find the work done for the process of the area of piston is 500cm2 and it moves out by 50 cm against a pressure of 1 atm during the reaction.
Zn(s)+2H+(aq)⇔Zn2+(aq)+H2(g)
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionAt 300 K, 4 gm calcium is dissolved in hydrochloric acid in an open vessel at the atmoshphere pressure 0.821 atm. Calculate work done by the system.
View Solution4g of NaOH was dissolved in one litre of a solution containing one mole of acetic acid and one mole of sodium acetete. Find the pH of the resulting solution (Ka of acetic acid is 1.8×10−3)
View SolutionAn ideal gas (γ=1.67) is taken through the process abc shown in figure . The temperature at the point a is 300k. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
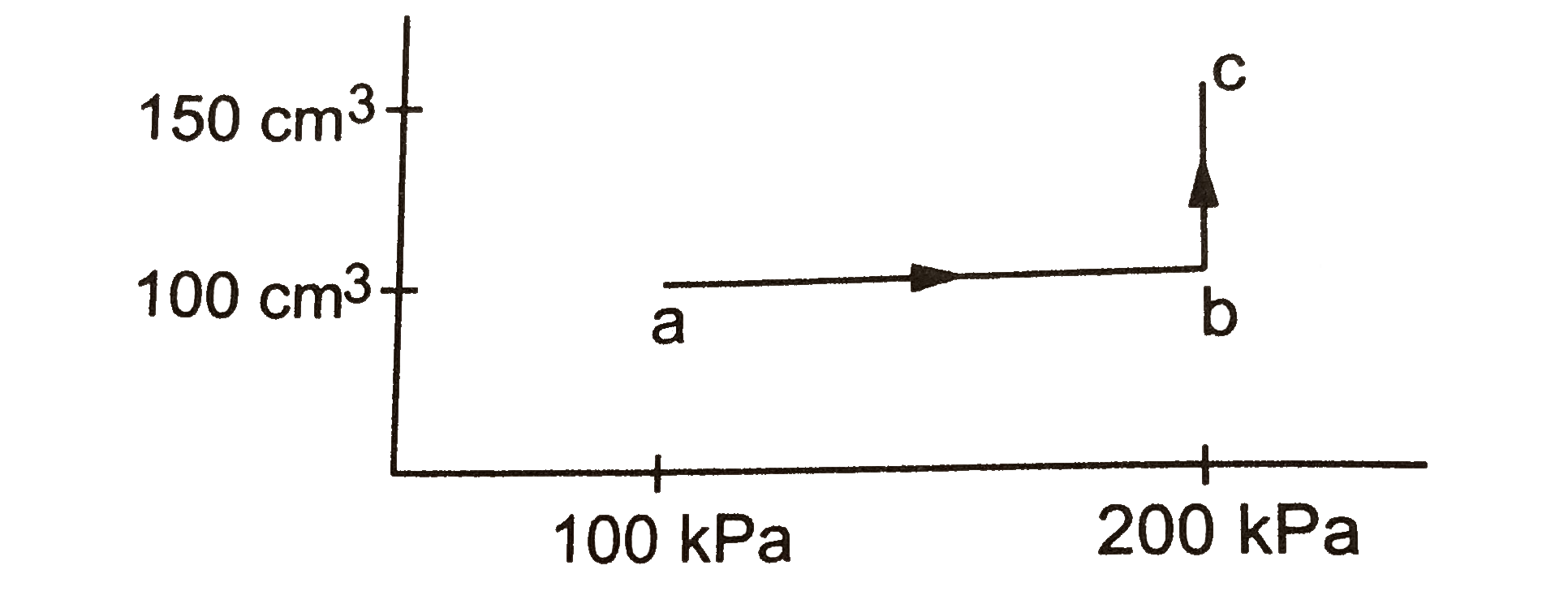
View SolutionA particle of mass 'm' is raised from the surface of earth to a height h = 2R. Find work done by some external agent in the process. Here, R is the radius of earth and g the acceleration due to gravity on earth's surface.
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.
View Solution
