When is more power delivered to a light bulb, just after it is turned on and the glow of the filament is increasing or after it has been ON for a few seconds and the glow is steady?
To determine when more power is delivered to a light bulb, we need to analyze the behavior of the filament when the bulb is first turned on versus after it has been on for a few seconds.
1. Initial Condition: When the light bulb is first turned on, the filament is cold. At this stage, the resistance of the filament is low.
Hint: Remember that resistance in a filament changes with temperature.
2. Current Flow: Since the resistance is low, according to Ohm's Law (V = IR), the current flowing through the filament will be high.
Hint: Think about how voltage, current, and resistance are related.
3. Power Calculation: The power delivered to the bulb can be calculated using the formula:
P=I2R
Since the current (I) is high and the resistance (R) is low, the power (P) delivered to the bulb is relatively large at this moment.
Hint: Recall that power is proportional to the square of the current.
4. Filament Heating: As the filament heats up, its resistance increases due to the temperature coefficient of resistance for the material (usually tungsten).
Hint: Consider how materials behave when they are heated.
5. Steady State Condition: After a few seconds, when the filament reaches a steady glow, the resistance is now higher, and consequently, the current flowing through the filament decreases.
Hint: What happens to current when resistance increases?
6. Power After Heating: With the increased resistance and decreased current, the power delivered to the bulb decreases.
Hint: Use the power formula again to see how changes in current and resistance affect power.
Conclusion:
More power is delivered to the light bulb just after it is turned on when the glow of the filament is increasing, compared to after it has been on for a few seconds when the glow is steady.
Final Answer: More power is delivered just after it is turned on.
P=I2R
Since the current (I) is high and the resistance (R) is low, the power (P) delivered to the bulb is relatively large at this moment.
More power is delivered to the light bulb just after it is turned on when the glow of the filament is increasing, compared to after it has been on for a few seconds when the glow is steady.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-0 LONG ANSWER TYPE3videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-115videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-0 SHORT ANSWER TYPE9videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F10videos
CURRENT ELECTRICITY
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )31videos
DYNAMICS OF A PARTICLE
Similar Questions
When is the higher rate of energy being delivered to a light bulb higher : just after it is turned on, the glow of the filament is increasing, or after it has been on for a few seconds and the glow is steady ?
View SolutionFind the current through the battery
(i) just after the switch is closed.
(ii) long after the switch has been closed.
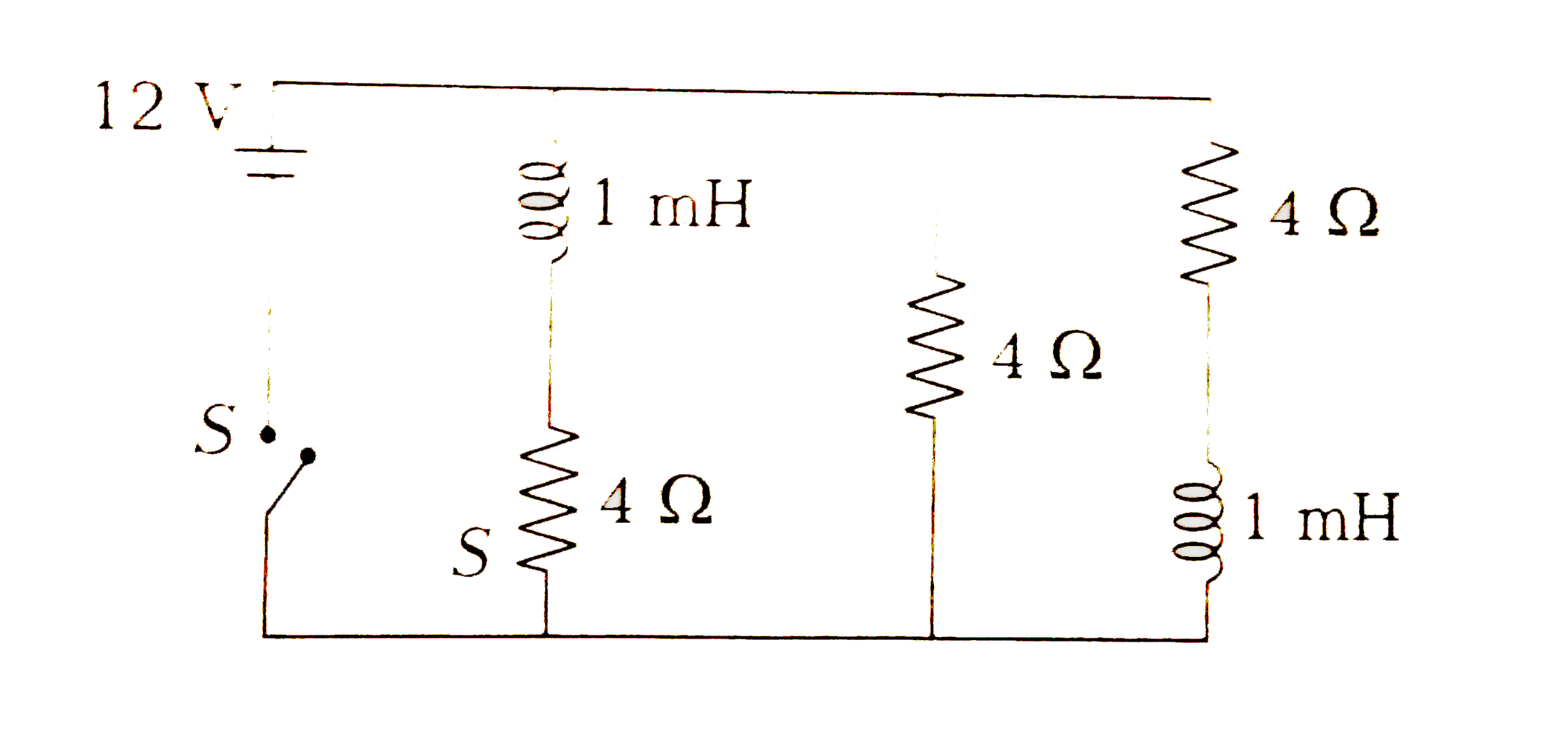View Solution
Knowledge Check
- Question 1 - Select One
The resistance of wire in a heater at room temperature is 65Oemga. When the heater is connected to a 220V supply the current settles after a few seconds to 2.8A. What is the steady temperature of the wire. (Temperature coefficient of resistance α=1.70×10−4^(∘).C−)
A955∘CB1055∘CC1155∘CD1258∘C
A small, circular ring is inside a larger loop that is connected to a battery and a switch as shown in Fig. 3.25. Use Lenz's law to find the direction of the current induced in the small ring
(a) just after switch S is closed,
(b) after Shas been closed for a long time,
( c) just after S has been reopened after being closed for a long time. ltbr>
View SolutionA metal block of heat capacity 90J/.∘C placed in a room at 25∘C is heated electrically. The heater is switched off when the temperature reaches 35∘C. The temperature of the block rises at the rate of 2∘C/s just after the heater is switched on and falls at the rate of 0.2∘C/s just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is 30∘C. (d) Assuming that the power radiated at 30∘C respresents the average value in the heating process, find the time for which the heater was kept on.
View SolutionA swimming pool is to be drained by cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L=2000(10−t)2. How fast is the water ruining out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
View SolutionA swimming pool is to be drained by cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L=2000(10−t)2. How fast is the water ruining out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
View SolutionA swimming pool is to be drained by cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L=2000(10−t)2. How fast is the water ruining out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
View SolutionA swimming pool is to be drained by cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L=2000(10−t)2. How fast is the water ruining out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
View SolutionBlock A has a mass 3kg and is sliding on a rough horizontal surface with a velocity uA=2m/s when it makes a direct collision with block B, which has a mass of 2kg and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is μk=0.3 ( Take g=10m/s2)
View Solution