The thermal coefficient of resistivity for a material is 10−3/∘C. A potential difference 100 V is applied across a conductor made out of this material at 20∘C. Initially, the rate of total heat dissipation in the conductor is H0. After some time, the conductor achieves an equilibrium temperature 100∘C . The rate of total heat dissipation at this temperature is H .The ratio H0H is _____
To solve the problem, we need to find the ratio H0H, where H0 is the initial rate of heat dissipation and H is the rate of heat dissipation at the equilibrium temperature.
1. Understand the relationship between heat dissipation and resistance:
The rate of heat dissipation H in a conductor can be expressed using the formula:
H=V2R
where V is the potential difference and R is the resistance of the conductor.
2. Identify the initial conditions:
At 20∘C, the initial resistance R0 can be expressed as:
R0=R20=R0
Therefore, the initial heat dissipation H0 is:
H0=V2R0
3. Determine the change in resistance with temperature:
The resistance of the conductor changes with temperature according to the formula:
R=R0(1+αΔT)
where α is the thermal coefficient of resistivity and ΔT is the change in temperature. Given α=10−3∘C−1 and the temperature change from 20∘C to 100∘C, we have:
ΔT=100−20=80∘C
Thus, the new resistance R at 100∘C is:
R=R0(1+10−3×80)=R0(1+0.08)=R0×1.08
4. Calculate the heat dissipation at equilibrium temperature:
The heat dissipation at the equilibrium temperature H can now be expressed as:
H=V2R=V2R0×1.08
5. Find the ratio H0H:
Now, we can find the ratio of the initial heat dissipation to the heat dissipation at equilibrium:
H0H=V2R0V2R0×1.08=R0×1.08R0=1.08
Final Answer:
The ratio H0H is 1.08.
The rate of heat dissipation H in a conductor can be expressed using the formula:
H=V2R
where V is the potential difference and R is the resistance of the conductor.
At 20∘C, the initial resistance R0 can be expressed as:
R0=R20=R0
Therefore, the initial heat dissipation H0 is:
H0=V2R0
The resistance of the conductor changes with temperature according to the formula:
R=R0(1+αΔT)
where α is the thermal coefficient of resistivity and ΔT is the change in temperature. Given α=10−3∘C−1 and the temperature change from 20∘C to 100∘C, we have:
ΔT=100−20=80∘C
Thus, the new resistance R at 100∘C is:
R=R0(1+10−3×80)=R0(1+0.08)=R0×1.08
The heat dissipation at the equilibrium temperature H can now be expressed as:
H=V2R=V2R0×1.08
Now, we can find the ratio of the initial heat dissipation to the heat dissipation at equilibrium:
H0H=V2R0V2R0×1.08=R0×1.08R0=1.08
The ratio H0H is 1.08.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-1
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-2
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-4
15 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
A potential difference of 30V is applied between the ends of a conductor of length 100 m and resistance 0.5Ω . The conductor has a uniform cross-section. Find the total linear momentum of free electrons.
View SolutionThe temperature coefficient of resistivity of material is 0.0004/k. When the temperature of the material is increased by 50∘C, its resistivity increases by 2×10−8 ohm-m. The initial resistivity of the material in ohm-m is
View SolutionA potential difference 100 V is applied across a conductor which is a cylindrical shell of inner and outer diameter 2 cm and 4 cm respectively and length 10 cm. Current flows in a direction parallel to the axis of the conductor. If heat is dissipated in the conductor at the rate 15 W, the resistivity of the material of the conductor is _________ Ωm. [Take π=228]
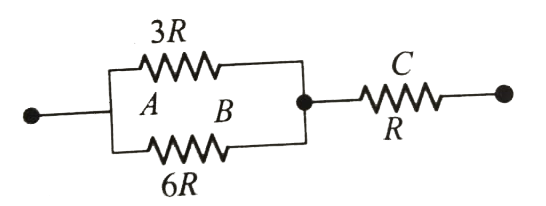
View SolutionFigure 7.37 shows a network of three resistances. When some potential difference is applied across the network , thermal powers dissipated by A,BandC are in the ratio
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionA wall has two layers A and B each made of different materials. The layer A is 10cm thick and B is 20 cm thick. The thermal conductivity of A is thrice that of B. Under thermal equilibrium temperature difference across the wall is 35∘C. The difference of temperature across the layer A is
View SolutionThe two ends of a metal rod are maintained at temperature 100∘C and 110∘C. The rate of heat flow in the rod is found to be 4.0J/s. If the ends are maintained at temperature s 200∘C and 210∘C. The rate of heat flow will be
View SolutionIf the resistance of a conductor is 5Ω at 50∘C and 7Ω at 100∘C then the mean temperature coefficient of resistance of the material is
View SolutionObjects A and B that are initially separated from each other and well isolated from their surroundings are then brought into thermal contact. Initially TA=0∘C and TB=100∘C . The specific heat of A is less than the specific heat of B. After some time, the system comes to an equilibrium state. the final temperatures are:
_E01_036_Q01.png)
View Solution
