The 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
5 s
10 s
50 s
100 s
The correct Answer is:C
To solve the problem, we need to determine the time interval required for a 500 µF capacitor to reach a potential difference of 10 V when charged at a steady rate of 100 µC/s.
1. Understand the relationship between charge, capacitance, and potential difference:
The potential difference (V) across a capacitor is given by the formula:
V=QC
where Q is the charge on the capacitor and C is the capacitance.
2. Identify the known values:
- Capacitance, C=500μF=500×10−6F
- Desired potential difference, V=10V
- Charging rate, dQdt=100μC/s=100×10−6C/s
3. Calculate the required charge (Q) for the desired potential difference:
Rearranging the formula for potential difference, we can find the charge:
Q=V×C
Substituting the known values:
Q=10V×500×10−6F=5000μC
4. Determine the time required to accumulate this charge at the given rate:
The charge accumulated over time t when charging at a rate of dQdt is given by:
Q=dQdt×t
Rearranging this gives:
t=QdQdt
Substituting the values we have:
t=5000μC100μC/s=50s
5. Conclusion:
The time interval required for the capacitor to reach a potential difference of 10 V is 50 seconds.
Final Answer:
The potential difference across the capacitor will be 10 V after an interval of 50 seconds.
---
The potential difference (V) across a capacitor is given by the formula:
V=QC
where Q is the charge on the capacitor and C is the capacitance.
- Capacitance, C=500μF=500×10−6F
- Desired potential difference, V=10V
- Charging rate, dQdt=100μC/s=100×10−6C/s
Rearranging the formula for potential difference, we can find the charge:
Q=V×C
Substituting the known values:
Q=10V×500×10−6F=5000μC
The charge accumulated over time t when charging at a rate of dQdt is given by:
Q=dQdt×t
Rearranging this gives:
t=QdQdt
Substituting the values we have:
t=5000μC100μC/s=50s
The time interval required for the capacitor to reach a potential difference of 10 V is 50 seconds.
The potential difference across the capacitor will be 10 V after an interval of 50 seconds.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
given that potential differene across 1μF capacitor is 10V. Then,
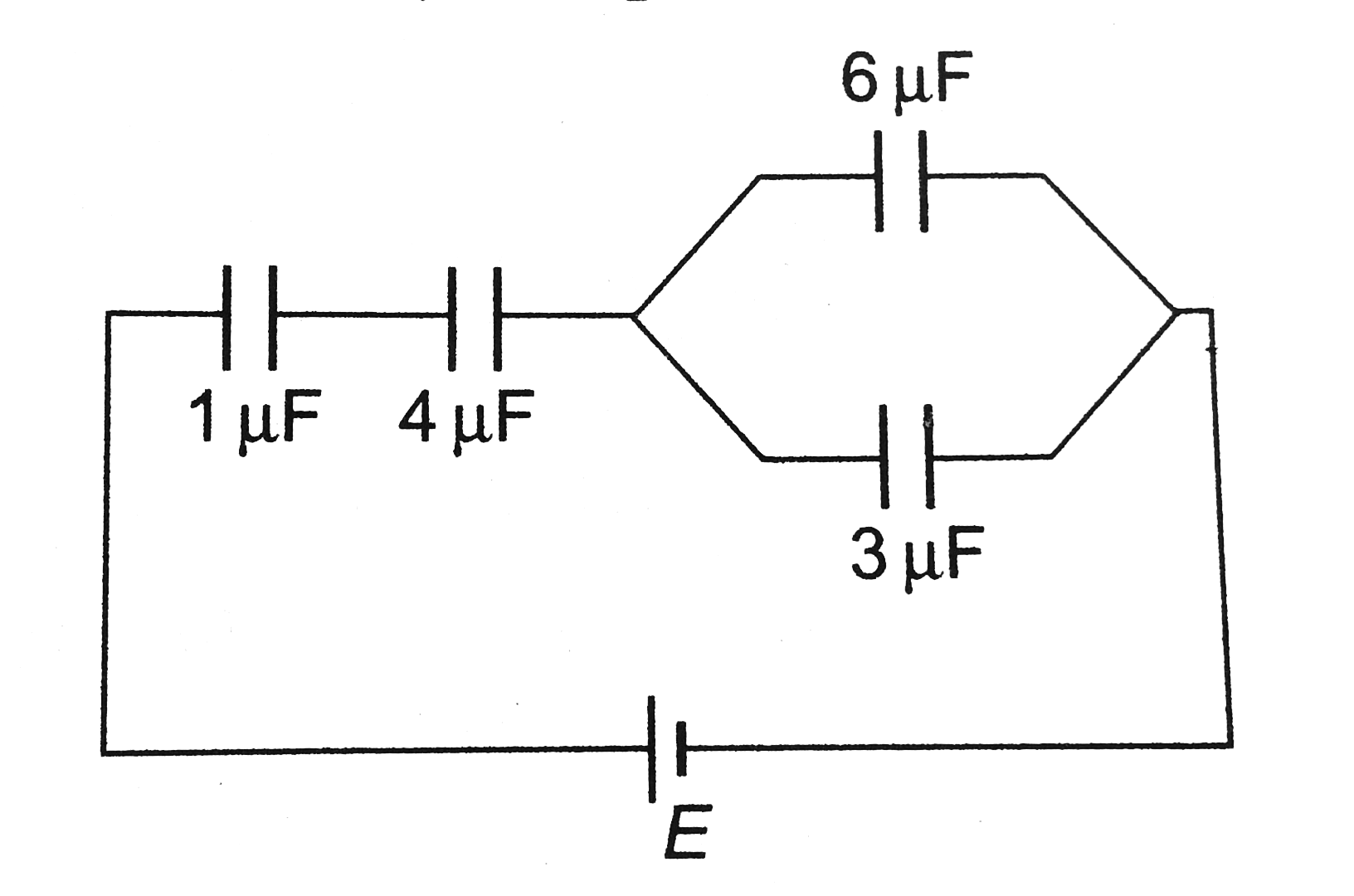
View SolutionThe potential drop across 7μF capacitor is 6V. Then
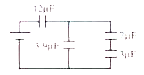
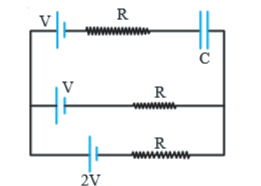
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
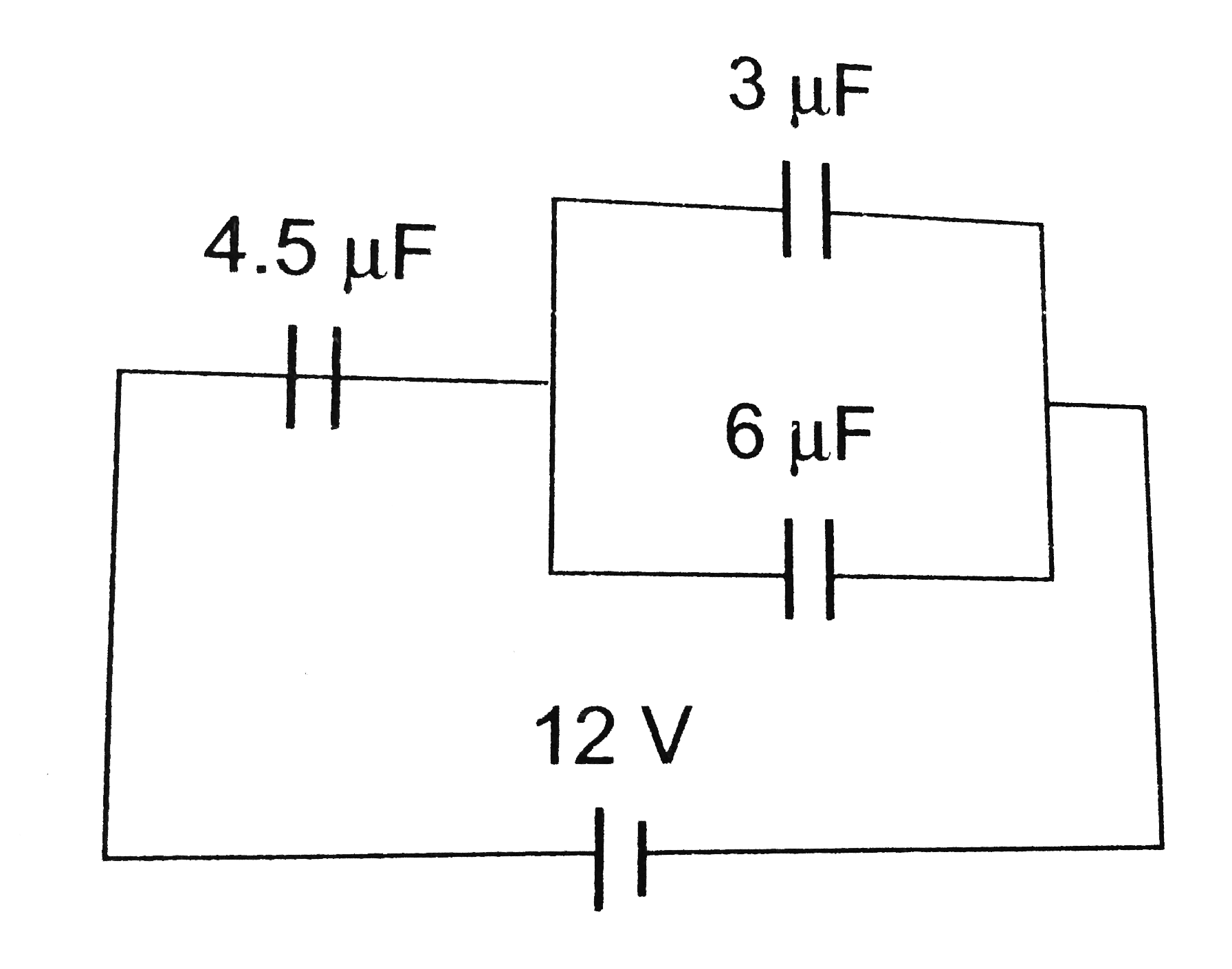
View SolutionIn the adjoning figure, the potential difference across the 4.5μF capacitor is

View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
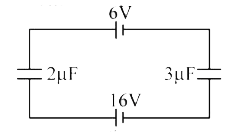
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
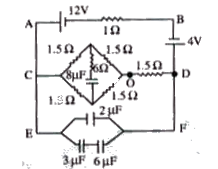
View SolutionFind charge on each capacitor and potential difference across each capacitor .

View SolutionThe charge on the 4μF capacitor in the steady state is
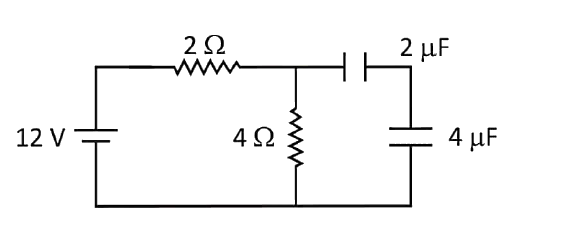
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
View SolutionA capacitor is charged steadily from a DC source. Correct variation of potential difference across the plates of capacitor with charge on the plates of capacitor is
View Solution
