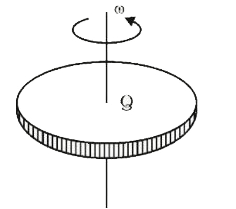
A non-conducting ring of radius R has charge Q distributed unevenly over it. If it rotates with an angular velocity ω the equivalent current will be:
zero
Qω
Qω2π
Qω2πr
The correct Answer is:c
Rotating charge is equivalent to current
I=QT where=T =time period =2ipω, Hence I=Qω2π
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-2
Explore 10 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-3
Explore 10 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET -5
Explore 15 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
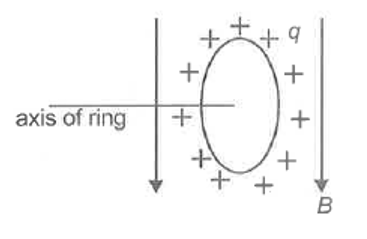
As shown in figure there is a ring having radius R and charge q distributed uniformly over it. If ring is rotated with a constant angular velocity @, then torque acting on the ring due to magnetic force is (Assume that magnetic field B is parallel to plane of ring)
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Let ring in the above question is having a radius R and a charge Q is uniformly distributed over it. Ring is rotated with a constant angular velocity (ω) as mentioned above.
Torque acting on the ring due to magnetic force is
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
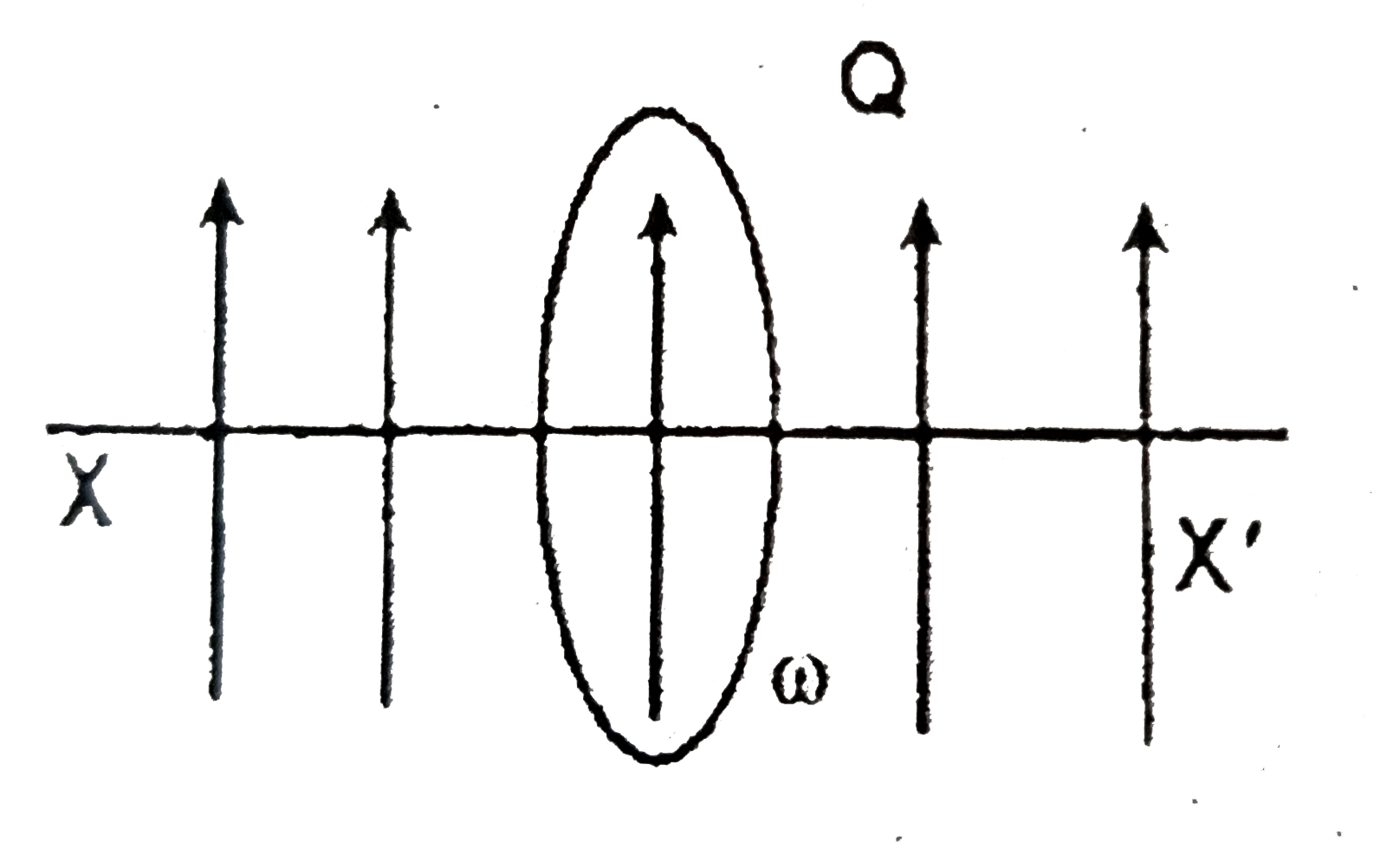
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View Solutionconsider a nonconducting ring of radius r and mass m which has a total charge q distributed uniformly on it the ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring (b) find the magnetic moment μ of the . (c) show thatμ=q2m where l is the angular momentum of the ring about its axis of rotation.
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

View Solution
