Two wires of different materials of resistivity , length , and area of cross-section respectively are connected in parallel. The ratio of current density in the two wires, , is given by:
To find the ratio of current density in two wires connected in parallel, we can follow these steps:
Step 1: Understand the relationship between current density, resistivity, and electric field
The current density j in a conductor is given by the equation:
j=σE
where σ is the conductivity of the material and E is the electric field. Conductivity σ is the reciprocal of resistivity ρ:
σ=1ρ
Thus, we can rewrite the current density as:
j=Eρ
Step 2: Relate electric field to voltage and length
For a wire, the electric field E can be expressed in terms of the voltage V across the wire and its length L:
E=VL
Substituting this into the equation for current density gives:
j=VρL
Step 3: Set up the equations for the two wires
For wire 1, we have:
j1=Vρ1L1
For wire 2, we have:
j2=Vρ2L2
Step 4: Find the ratio of current densities
Now, we can find the ratio of the current densities j1j2:
j1j2=Vρ1L1Vρ2L2=ρ2L2ρ1L1
Step 5: Simplify the expression
The voltage V cancels out, leading to the final expression:
j1j2=ρ2L2ρ1L1
Conclusion
The ratio of current densities in the two wires is given by:
j1j2=ρ2L2ρ1L1
The current density j in a conductor is given by the equation:
j=σE
where σ is the conductivity of the material and E is the electric field. Conductivity σ is the reciprocal of resistivity ρ:
σ=1ρ
Thus, we can rewrite the current density as:
j=Eρ
For a wire, the electric field E can be expressed in terms of the voltage V across the wire and its length L:
E=VL
Substituting this into the equation for current density gives:
j=VρL
For wire 1, we have:
j1=Vρ1L1
For wire 2, we have:
j2=Vρ2L2
Now, we can find the ratio of the current densities j1j2:
j1j2=Vρ1L1Vρ2L2=ρ2L2ρ1L1
The voltage V cancels out, leading to the final expression:
j1j2=ρ2L2ρ1L1
The ratio of current densities in the two wires is given by:
j1j2=ρ2L2ρ1L1
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-2
Explore 10 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-3
Explore 10 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET -5
Explore 15 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
Knowledge Check
Two inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
The ratio of current i1/i2 is?
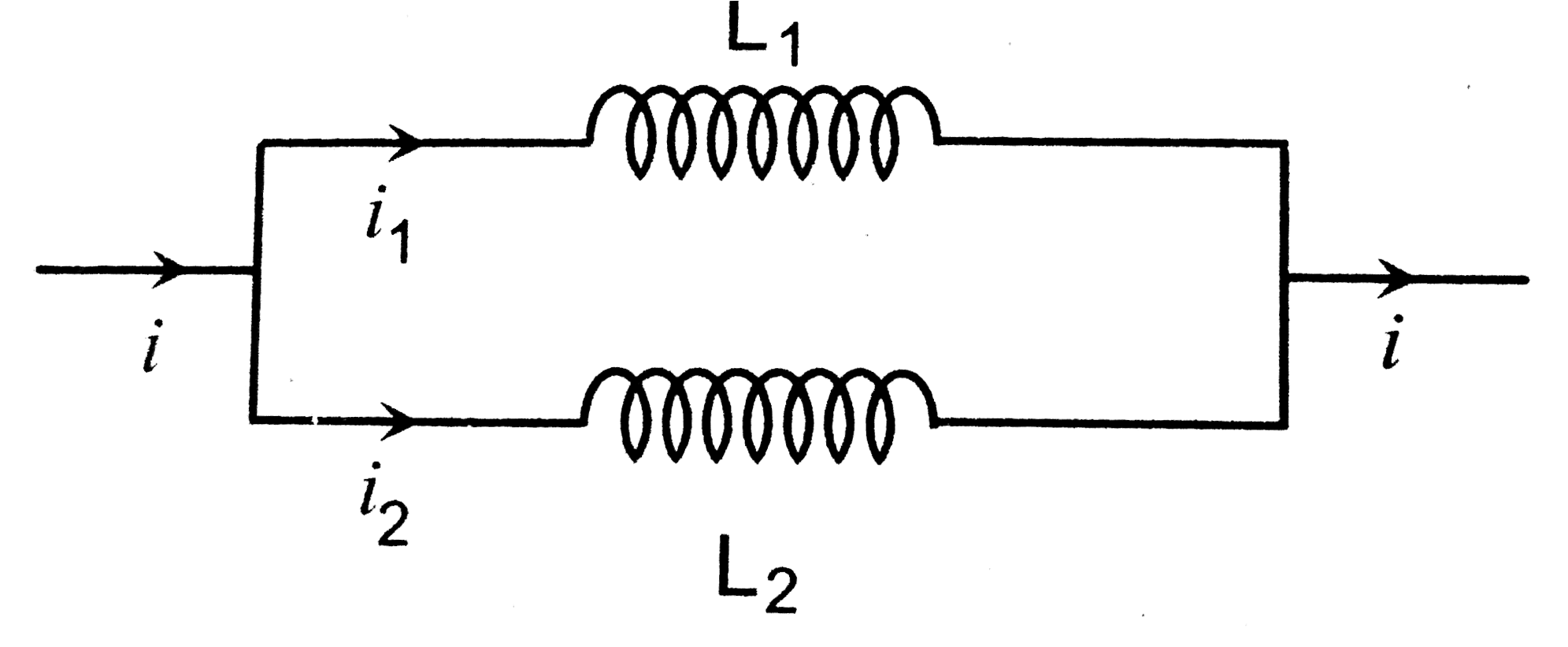 AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2
AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2
The wire of same dimension but resistivities(p1) and (p2)are connected in parallel. The equivalent resistivity of the combination is
View SolutionTwo inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2

View SolutionTwo concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
View SolutionWe have two (narrow) capillary tubes T1 and T2 . Their lengths are l1 and l2 and radii of cross-section are r1 and r2 respectively. The rate of flow of water under a pressure difference P through tube T is 8cm3/sec. If l1=2l2 and r1=r2 what will be the rate of flow when the two tubes are connected in series and pressure difference across the combinatin is same as before (=P)
View SolutionConsider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
View SolutionTwo metallic wires. A and B of equal dimensions but made of different materials, having resistivities p and 2p temperature coefficients of resistivities 2aipha and α, are connected in series. The temperature coefficient of resistance of the composite wire equals
View SolutionTwo metallic wires of the same material B, have the same length out cross-sectional area is in the ratio 1:2. They are connected (i) in series and (ii) in parallel. Compare the drift velocities of electrons in the two wires in both the cases (i) and (ii) .
View Solution