A car battery with a 12V e.m.f. and an internal resistance of 0.04Ω is being charged with a current of 50A.
The rate at which energy is being dissipated as heat inside the battery is:
100W
500W
600W
700W
To find the rate at which energy is being dissipated as heat inside the battery, we can use the formula for power dissipated due to resistance in an electrical circuit. The power (P) dissipated in a resistor can be calculated using the formula:
P=I2R
Where:
- P is the power in watts (W),
- I is the current in amperes (A),
- R is the resistance in ohms (Ω).
1. Identify the given values:
- E.M.F of the battery, V=12V (not directly needed for this calculation),
- Internal resistance of the battery, r=0.04Ω,
- Current flowing through the battery, I=50A.
2. Use the power formula:
We will use the formula for power dissipation due to internal resistance:
P=I2R
3. Substitute the values into the formula:
P=(50A)2×0.04Ω
4. Calculate I2:
I2=502=2500A2
5. Multiply by the internal resistance:
P=2500A2×0.04Ω
6. Perform the multiplication:
P=2500×0.04=100W
7. Conclusion:
The rate at which energy is being dissipated as heat inside the battery is 100W.
Final Answer:
The rate at which energy is being dissipated as heat inside the battery is 100 watts.
- P is the power in watts (W),
- I is the current in amperes (A),
- R is the resistance in ohms (Ω).
- E.M.F of the battery, V=12V (not directly needed for this calculation),
- Internal resistance of the battery, r=0.04Ω,
- Current flowing through the battery, I=50A.
We will use the formula for power dissipation due to internal resistance:
P=I2R
P=(50A)2×0.04Ω
I2=502=2500A2
P=2500A2×0.04Ω
P=2500×0.04=100W
The rate at which energy is being dissipated as heat inside the battery is 100W.
The rate at which energy is being dissipated as heat inside the battery is 100 watts.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-3
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-4
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-1
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
A car battery with a 12V e.m.f. and an internal resistance of 0.04Ω is being charged with a current of 50A.
The potential difference V across the terminals of the battery are:
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View Solution
Knowledge Check
A battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
A7Ω,7VB8Ω,8VC9Ω,9VD9Ω,10V
A battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionA storage battery of emf 8.0 V and internal resistance 0.5Ω is being charged by a 120V dc supply using a series resistor of 15.5Ω. what in the terminal voltage of the battery during charging ? What is the purpose of having a series resistor in the charging circuit?
View SolutionAn ideal voltmeter V is connected to a 2.0Ω resistor and a battery with emf 5.0V and internal resistance 0.5Ω as shown in figure
(a) What is the current in the 2.0Ω resistor?
(b) What is the terminal voltage of the battery?
(c) What is the reading of the voltmeter?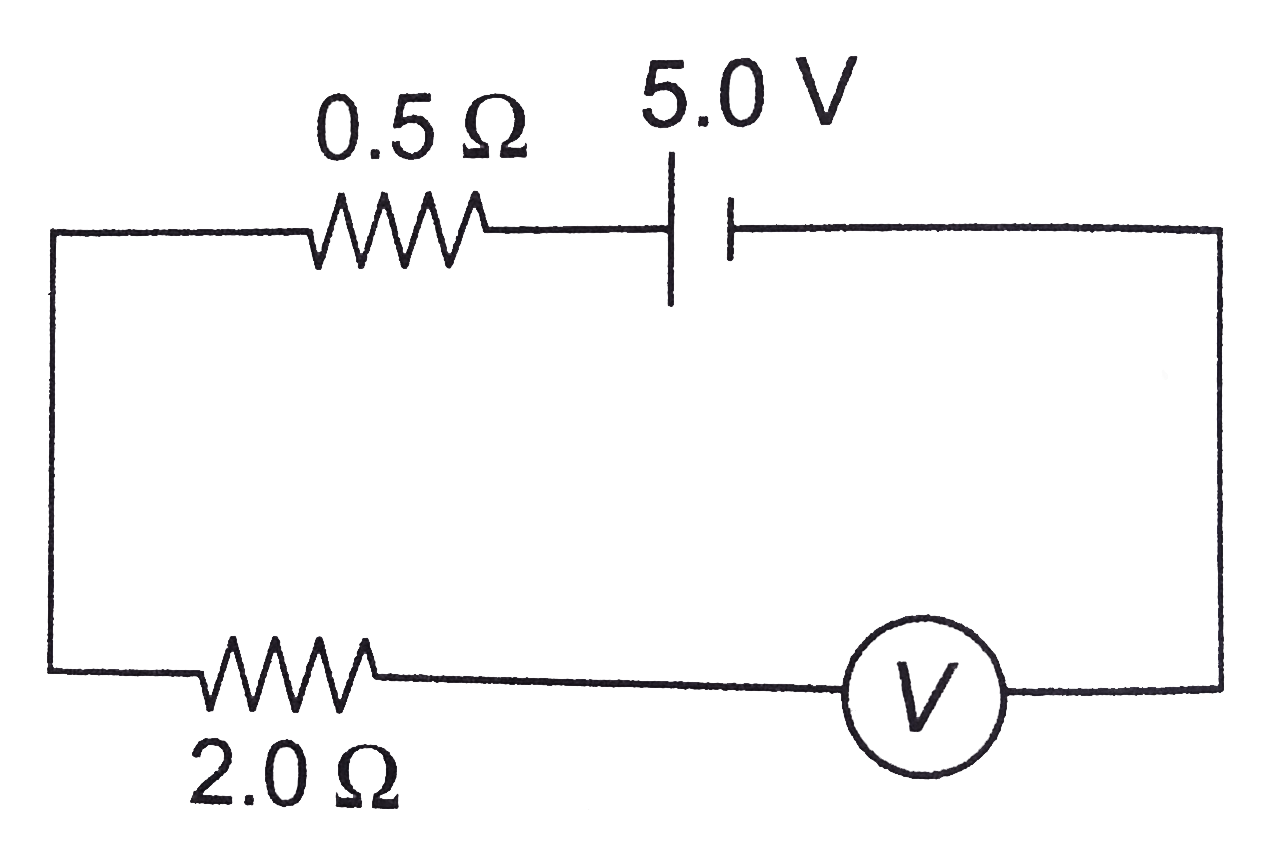
View SolutionA car battery of emf 12V and internal resistance 0.05ω receives a current of 60 A from an external source, then the terminal potential difference of the battery is
View SolutionA battery of six cells each of e.m.f . 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω. What is the potential difference across the battery?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionIn the circuit shown in figure a 12V battery with unknown internal resistance r is connected to another battery with unknown emf E and internal resistance 1Ω and to a resistance of 3Ω carrying a current of 2A. The current through the rechargeable battery is 1A in the direction shown. Figure the unknown current i internal resistance r and the emf E.
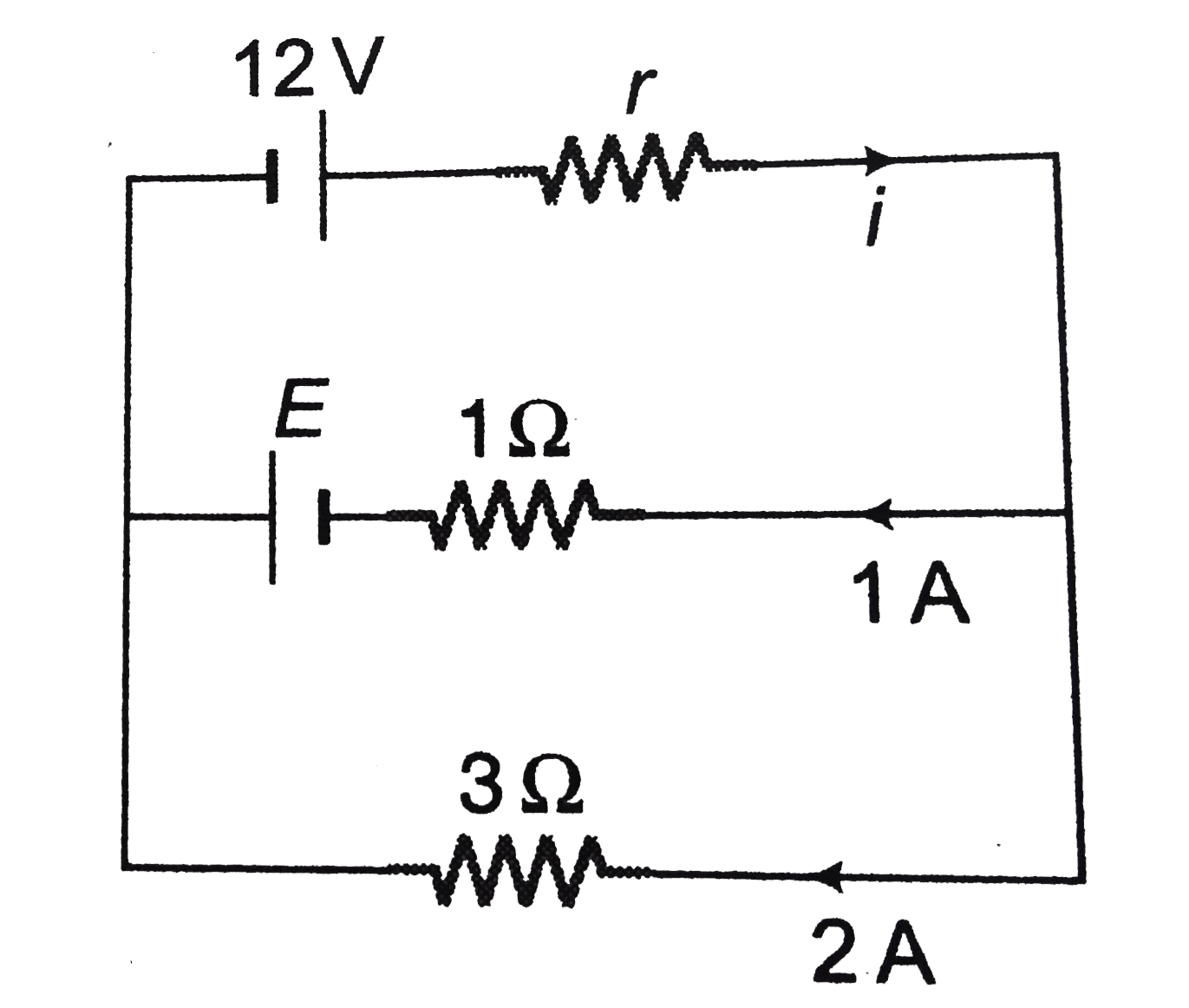
View Solution
