A heater coil is cut into two parts of equal length and one of them is used in the leader. The ratio of the heat procued by this half coil to that by the original coil is
2:1
1:2
1:4
4:1
To solve the problem of finding the ratio of heat produced by half of the heater coil to that produced by the original coil, we can follow these steps:
Step 1: Understand the relationship between power, resistance, and heat produced.
The heat produced (H) in a resistor (or coil) is given by the formula:
H=P×t
where P is the power and t is the time for which the power is applied.
Step 2: Relate power to resistance.
The power P can also be expressed in terms of voltage V and resistance R:
P=V2R
From this, we can see that power is inversely proportional to resistance.
Step 3: Determine the resistance of the original coil and the half coil.
Let the length of the original coil be L. The resistance R of a wire is given by:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
When the coil is cut in half, the length of one part becomes L2. Therefore, the resistance of the half coil R1 is:
R1=ρL/2A=R2
where R is the resistance of the original coil.
Step 4: Calculate the power for both coils.
Using the power formula:
- For the original coil:
Poriginal=V2R
- For the half coil:
Phalf=V2R1=V2R2=2V2R
Step 5: Find the ratio of power.
Now, we can find the ratio of the power produced by the half coil to that produced by the original coil:
PhalfPoriginal=2V2RV2R=2
Step 6: Relate heat produced to power.
Since heat produced is directly proportional to power for the same time duration, the ratio of heat produced by the half coil to that produced by the original coil is the same as the ratio of their powers:
HhalfHoriginal=PhalfPoriginal=2
Conclusion:
Thus, the ratio of the heat produced by the half coil to that produced by the original coil is:
Ratio=2:1
---
The heat produced (H) in a resistor (or coil) is given by the formula:
H=P×t
where P is the power and t is the time for which the power is applied.
The power P can also be expressed in terms of voltage V and resistance R:
P=V2R
From this, we can see that power is inversely proportional to resistance.
Let the length of the original coil be L. The resistance R of a wire is given by:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
R1=ρL/2A=R2
where R is the resistance of the original coil.
Using the power formula:
- For the original coil:
Poriginal=V2R
- For the half coil:
Phalf=V2R1=V2R2=2V2R
Now, we can find the ratio of the power produced by the half coil to that produced by the original coil:
PhalfPoriginal=2V2RV2R=2
Since heat produced is directly proportional to power for the same time duration, the ratio of heat produced by the half coil to that produced by the original coil is the same as the ratio of their powers:
HhalfHoriginal=PhalfPoriginal=2
Thus, the ratio of the heat produced by the half coil to that produced by the original coil is:
Ratio=2:1
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-5
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
A heater coil is cut into two equal parts and only one part is now used in the heater. The heat generated will now be
View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View Solution
Knowledge Check
A heater coil is rated 100W,200V. It is cut into two identical parts. Both parts are connected together in parallel, to the same sources of 200V. Calculate the energy liberated per second in the new combination.
A100JB200JC300JD400J
A circular coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2. Current I remaining the same. Calculate the ratio of the magnetic moments of the new coil and the original coil.
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
View SolutionThe power of a heating coil is P. It is cut into two equal parts. The power of one of them across same mains is :
View SolutionThe magnetic field induction at the centre of a current - carrying circular coil (coil 1) and a closed coil (coil 2), shaped as a quarter of a disc is found to be equal in magnitude. If both the coils have equal area, then find the ratio of the currents flowing in coil 2 and coil 1.
View SolutionA heater coil is rated 100W,200V. It is cut into two identical parts. Both parts are connected together in parallel, to the same sources of 200V. Calculate the energy liberated per second in the new combination.
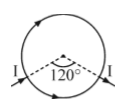
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
View SolutionWhen equal current is passed through two coils equal magnetic field is produced at their centers. If the ratio of number of turns in the coils is 8:15 then the ratio of the their radii will be
View Solution
