A battery has a variable EMF E depending on the amount of electrochemical energy stored in it, U : E=E0[VV0]13 , whereE0 is the EMF of the battery when it has the maximum possible energy, V0 , stored in it. The internal resistance of the battery is negligible. The battery, with energy stored in it, is connected with a resistance R and the switch is closed at . Choose the correct option(s):
The EMF of the battery decreases linearly with time
The rate of heat dissipation in the resistance decreases linearly with time
The energy stored in the battery runs out at t=3V0RE20
The total heat dissipated in the resistance until t=3V0R2E20is78V0
To solve the problem, we need to analyze the relationship between the electromotive force (EMF) of the battery, the energy stored in it, and the time as the battery discharges through a resistor.
1. Understand the EMF Equation:
The EMF of the battery is given by:
E=E0(VV0)1/3
where E0 is the maximum EMF when the battery is fully charged with energy V0.
2. Power Dissipation in the Resistor:
The power P dissipated in the resistor R is given by:
P=E2R
This power is also equal to the rate of change of energy stored in the battery:
P=−dVdt
Therefore, we can equate the two expressions:
−dVdt=E2R
3. Substituting for EMF:
Substitute the expression for E into the power equation:
−dVdt=E20R(VV0)2/3
4. Rearranging the Equation:
Rearranging gives:
−dV=E20R(VV0)2/3dt
5. Integrating:
Integrate both sides. The limits for V will be from V0 to V and for t from 0 to t:
∫VV0−dV=E20R∫t0(VV0)2/3dt
6. Solving the Integral:
After integrating, we find:
3V1/3−3V1/30=−E20t3RV2/30
7. Finding the Expression for EMF:
From the integrated equation, we can express V in terms of t:
V1/3=V1/30−E20t9RV2/30
Then substituting back into the EMF equation gives us:
E=E0(VV0)1/3
8. Analyzing the Options:
- Option A: The EMF of the battery decreases linearly with time. This is true based on the derived equation.
- Option B: The rate of heat dissipation decreases linearly with time. This is false since it depends on the square of the EMF.
- Option C: The energy stored in the battery runs out at T=3V0RE20. This is true.
- Option D: The total heat dissipated until T=3V0RE20 is 7V08. This is also true.
Conclusion:
The correct options are A, C, and D.
The EMF of the battery is given by:
E=E0(VV0)1/3
where E0 is the maximum EMF when the battery is fully charged with energy V0.
The power P dissipated in the resistor R is given by:
P=E2R
This power is also equal to the rate of change of energy stored in the battery:
P=−dVdt
Therefore, we can equate the two expressions:
−dVdt=E2R
Substitute the expression for E into the power equation:
−dVdt=E20R(VV0)2/3
Rearranging gives:
−dV=E20R(VV0)2/3dt
Integrate both sides. The limits for V will be from V0 to V and for t from 0 to t:
∫VV0−dV=E20R∫t0(VV0)2/3dt
After integrating, we find:
3V1/3−3V1/30=−E20t3RV2/30
From the integrated equation, we can express V in terms of t:
V1/3=V1/30−E20t9RV2/30
Then substituting back into the EMF equation gives us:
E=E0(VV0)1/3
- Option A: The EMF of the battery decreases linearly with time. This is true based on the derived equation.
- Option B: The rate of heat dissipation decreases linearly with time. This is false since it depends on the square of the EMF.
- Option C: The energy stored in the battery runs out at T=3V0RE20. This is true.
- Option D: The total heat dissipated until T=3V0RE20 is 7V08. This is also true.
The correct options are A, C, and D.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 JEE MAIN ARCHIVE
93 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-4
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
An inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
View SolutionIn Fig. 7.48, each of the segments (e.g.,AE,GM,etc.) has resistance r. A battery of emf V is connected between AandC. Internal resistance of the battery is negligible.

What is the equivalent resistance of the system about AandC?
View Solution
Knowledge Check
The battery of a trunk has an emf of 24 V. If the internal resistance of the battery is 0.8Ω. What is the maximum current that can be drawn from the battery?
A30AB32AC33AD34AA pure inductor L, a capactior C and a resistance R are connected across a battery of emf E and internal resistance r as shows in Fig. Switch SW is closed at t=0, select the correct altermative (S).
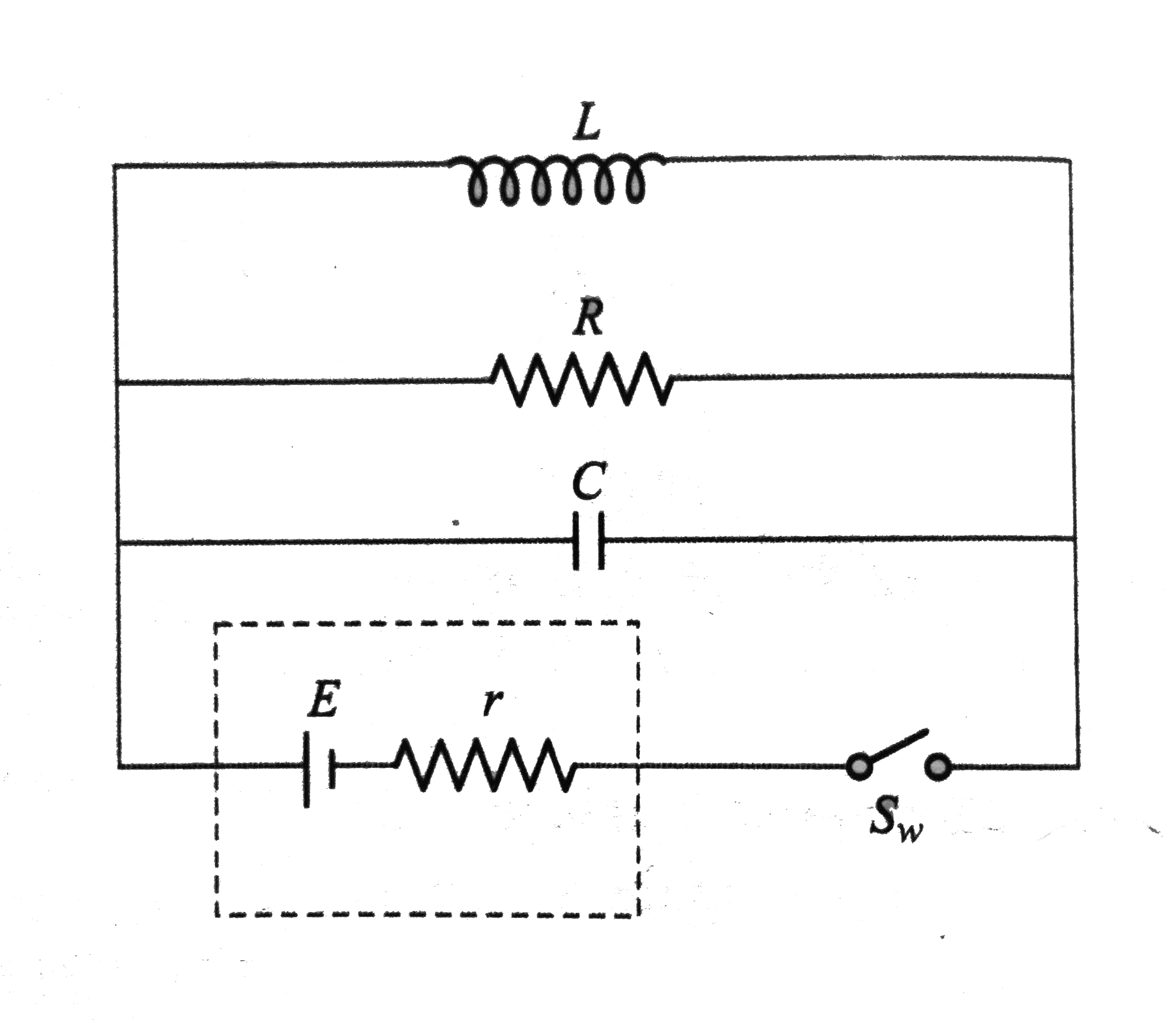 ACurrent through resistance R is zero all the time.BCurrent through resistance R is zero at t = 0 and t→∞.CMaximum charge stored in the capacitor is Cε.DMaximum energy stored in the inductor is equal to the maximum energy stored in the capacitor.
ACurrent through resistance R is zero all the time.BCurrent through resistance R is zero at t = 0 and t→∞.CMaximum charge stored in the capacitor is Cε.DMaximum energy stored in the inductor is equal to the maximum energy stored in the capacitor.
A 5 V battery with internal resistance 1Ω and a 2 V battery with internal resistance 0.5Ω are connected to a 3Ω resistor as shown in the figure.The current in the 3Ω resistor is
View SolutionIn Fig. 7.48, each of the segments (e.g.,AE,GM,etc.) has resistance r. A battery of emf V is connected between AandC. Internal resistance of the battery is negligible.
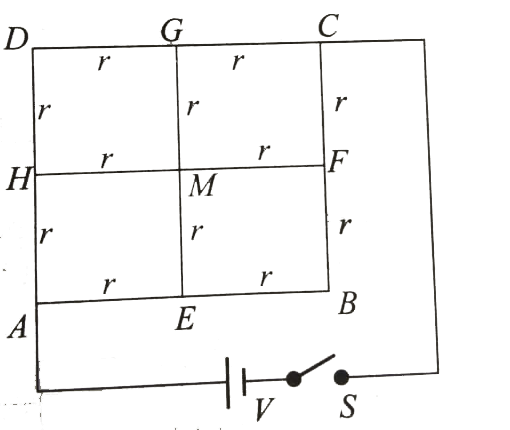
If a potentiometer circuit having gradient k is connected across the points HandC, the balancing length shown by the potentiometer is
View SolutionIn the adjoining circuit, the battery E1 has an e.m.f me of 12 volt and zero internal resistance while the battery E has an e.m.f me of 2volt . If the galvanometer G reads zero, then the value of the resistance X in ohm is

View SolutionIn the adjoining circuit, the battery E1 has an e.m.f me of 12 volt and zero internal resistance while the battery E has an e.m.f me of 2volt . If the galvanometer G reads zero, then the value of the resistance X in ohm is

View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionThe storage battery of a car has an emf of 12 V. If the internal resistance of the battery of 0.4Ω, What is the maximum current that can be drawn from the battery ?
View Solution

