If angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be also conserved ? Explain.
To solve the question, "If angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be also conserved? Explain," we can follow these steps:
Step 1: Understand Angular Momentum Conservation
- Angular momentum (L) is defined as the product of the moment of inertia (I) and the angular velocity (ω):
L=I⋅ω
- If angular momentum is conserved, it means that L remains constant over time.
Step 2: Analyze the Relationship Between Moment of Inertia and Angular Velocity
- Given that angular momentum is conserved (L = constant), if the moment of inertia (I) decreases, the angular velocity (ω) must adjust to keep L constant:
L=I1⋅ω1=I2⋅ω2
where I1 and I2 are the initial and final moments of inertia, and ω1 and ω2 are the corresponding angular velocities.
Step 3: Express Rotational Kinetic Energy
- The rotational kinetic energy (KE) of a rotating body is given by:
KE=12Iω2
Step 4: Substitute the Angular Momentum Relation
- Since L=I⋅ω is constant, we can express ω in terms of L and I:
ω=LI
- Substitute this into the kinetic energy formula:
KE=12I(LI)2=L22I
Step 5: Analyze the Effect of Decreasing Moment of Inertia
- From the expression KE=L22I, we see that kinetic energy is inversely proportional to the moment of inertia (I):
- If I decreases, KE increases.
Step 6: Conclusion
- Therefore, if the moment of inertia decreases while angular momentum is conserved, the rotational kinetic energy will not be conserved; instead, it will increase.
Final Answer:
In conclusion, if angular momentum is conserved in a system whose moment of inertia is decreased, the rotational kinetic energy will not be conserved; it will increase.
- Angular momentum (L) is defined as the product of the moment of inertia (I) and the angular velocity (ω):
L=I⋅ω
- If angular momentum is conserved, it means that L remains constant over time.
- Given that angular momentum is conserved (L = constant), if the moment of inertia (I) decreases, the angular velocity (ω) must adjust to keep L constant:
L=I1⋅ω1=I2⋅ω2
where I1 and I2 are the initial and final moments of inertia, and ω1 and ω2 are the corresponding angular velocities.
- The rotational kinetic energy (KE) of a rotating body is given by:
KE=12Iω2
- Since L=I⋅ω is constant, we can express ω in terms of L and I:
ω=LI
- Substitute this into the kinetic energy formula:
KE=12I(LI)2=L22I
- From the expression KE=L22I, we see that kinetic energy is inversely proportional to the moment of inertia (I):
- If I decreases, KE increases.
Step 6: Conclusion
- Therefore, if the moment of inertia decreases while angular momentum is conserved, the rotational kinetic energy will not be conserved; instead, it will increase.
In conclusion, if angular momentum is conserved in a system whose moment of inertia is decreased, the rotational kinetic energy will not be conserved; it will increase.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (SA-II Short Answer Type -II)12videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (LA: Long Answer Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
The angular momentum of body remains conserve if :
View SolutionThe angular momentum of a system of particles is conserved
View SolutionA bomb, initially at rest, explodes into several pieces. (a) Is linear momentum of the system conserved? (b) Is kinetic energy of the system conserved? Explain.
View SolutionThe moment of inertial of a rigid body in terms of its angular momentum L and kinetic energy K is
View SolutionKeeping moment of inertia constant, the angular momentum of a body is increased by 20%. The percentage increase in its rotational kinetic energy is
View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
View SolutionIf angular momentum of a body increased by 200% its kinetic energy will increase by :
View SolutionOn decreasing the heat, the kinetic energy of particles also decreases.
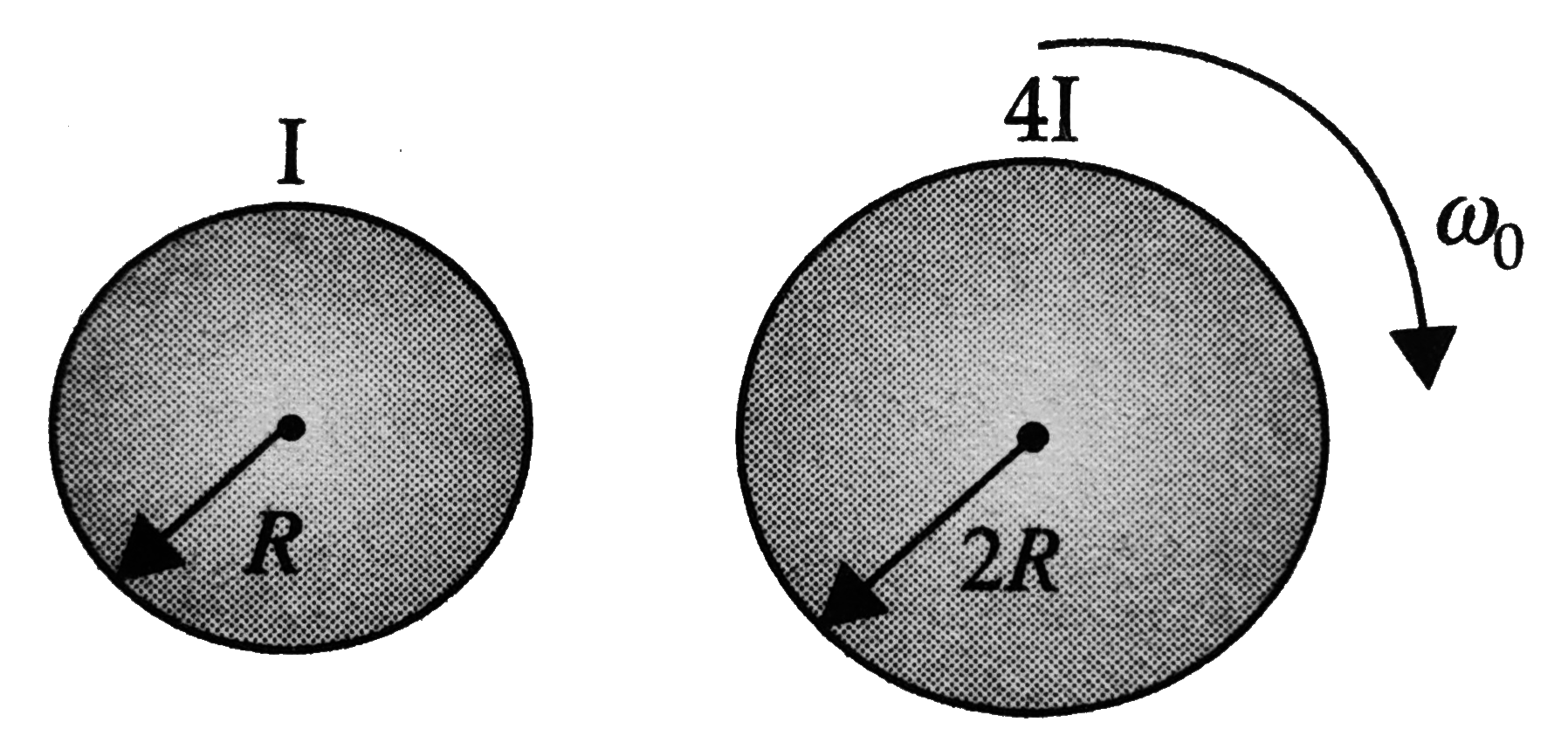
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
 View Solution
View SolutionIf the angular momentum of a body increases by 50%, its kinetic energy of rotation increases by
View Solution

