Three rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is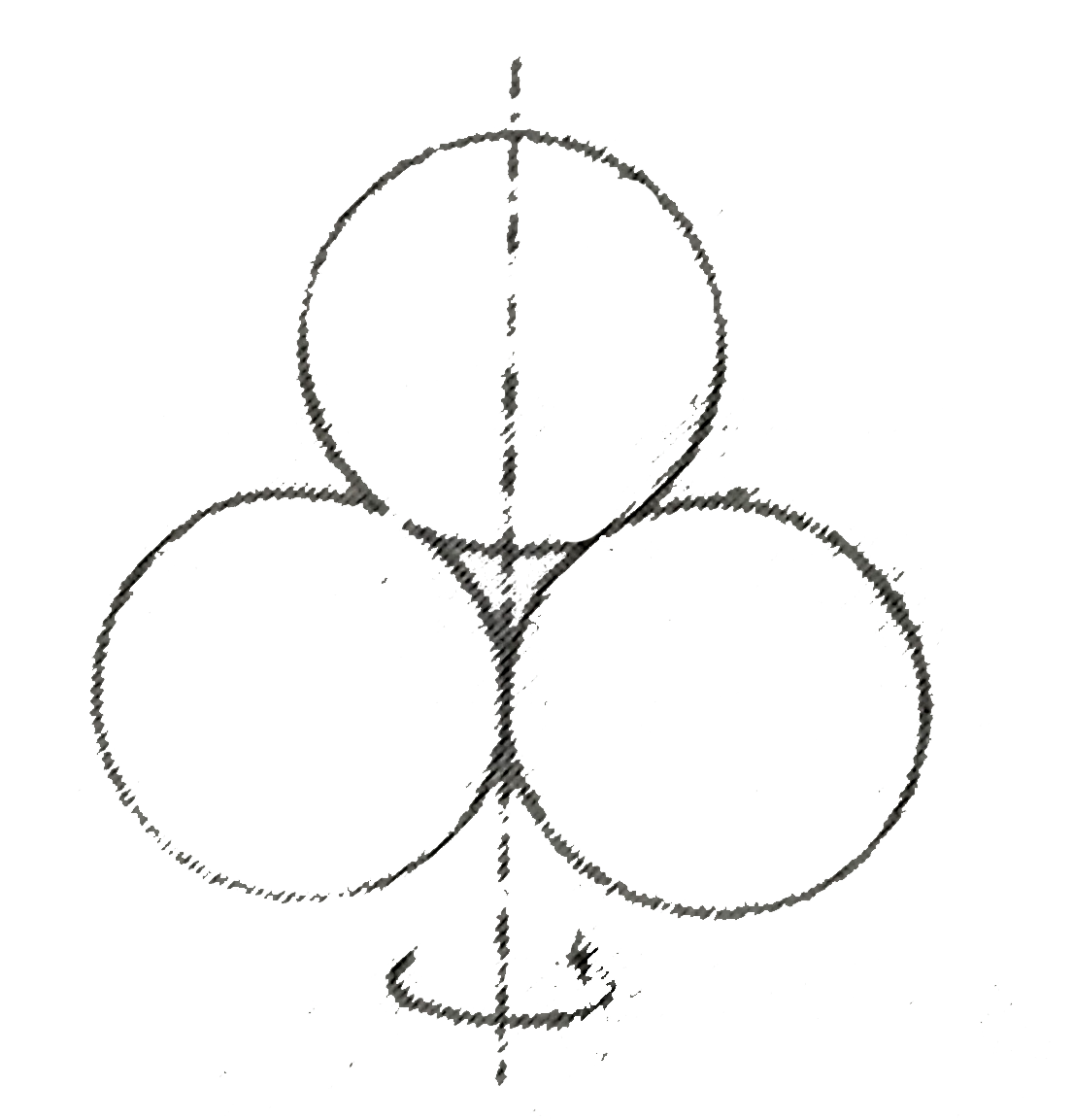 
√65r
√56r
√67r
√76 r
The correct Answer is:D
I=12mr2+2(12mr2+mr2)=72mr2=(3m)K2, where K = radius of gyration.
K=√76r
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Angular Momentum, Collision)15videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)15videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (LA: Long Answer Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
Three rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be
View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
View SolutionTwo rings of same mass and radius R are placed with their planes perpendicular to each other and centre at a common point. The radius of gyration of the system about an axis passing through the centre and perpendicular to the plane of one ring is
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionThe radius of gyration of a hollow sphere of radius R about an axis along its tangent is
View SolutionThe radius of gyration of a solid sphere of radius R about its tangent is
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring =m, radius=r)
View Solution