A wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wire frarne about the side BC is
11252mI2
8203mI2
5136mI2
7162mI2
The correct Answer is:D
ABBC=2∴AB=DC=13 and BC=AD=16
Similarly, mAB=mDC=m3 and mBC=mAD=m6
Now, I=2IAB+IAD+IBC
=2{m3(13)2.13}+(m6)(13)2+0=7162mI2

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Angular Momentum, Collision)15videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)15videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (LA: Long Answer Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
A wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
IN a retangle ABCD (BC = 2AB). The moment of inertia along which aixs will be minimum
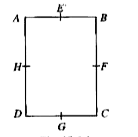 ABCBBDCHFDEG
ABCBBDCHFDEG - Question 2 - Select One
A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 Aml2BzeroCml2π2Dml22π2
Aml2BzeroCml2π2Dml22π2
A wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is
 View Solution
View SolutionChoose the correct option:
A wire of mass m and length l is bent in the form of a quarter circle. The moment of the inertia of the wire about an axis is passing through the centre of the quarter circle is approximatelyView SolutionIn a rectangle ABCD (BC=2AB). The moment of inertia along which axis will be minimum
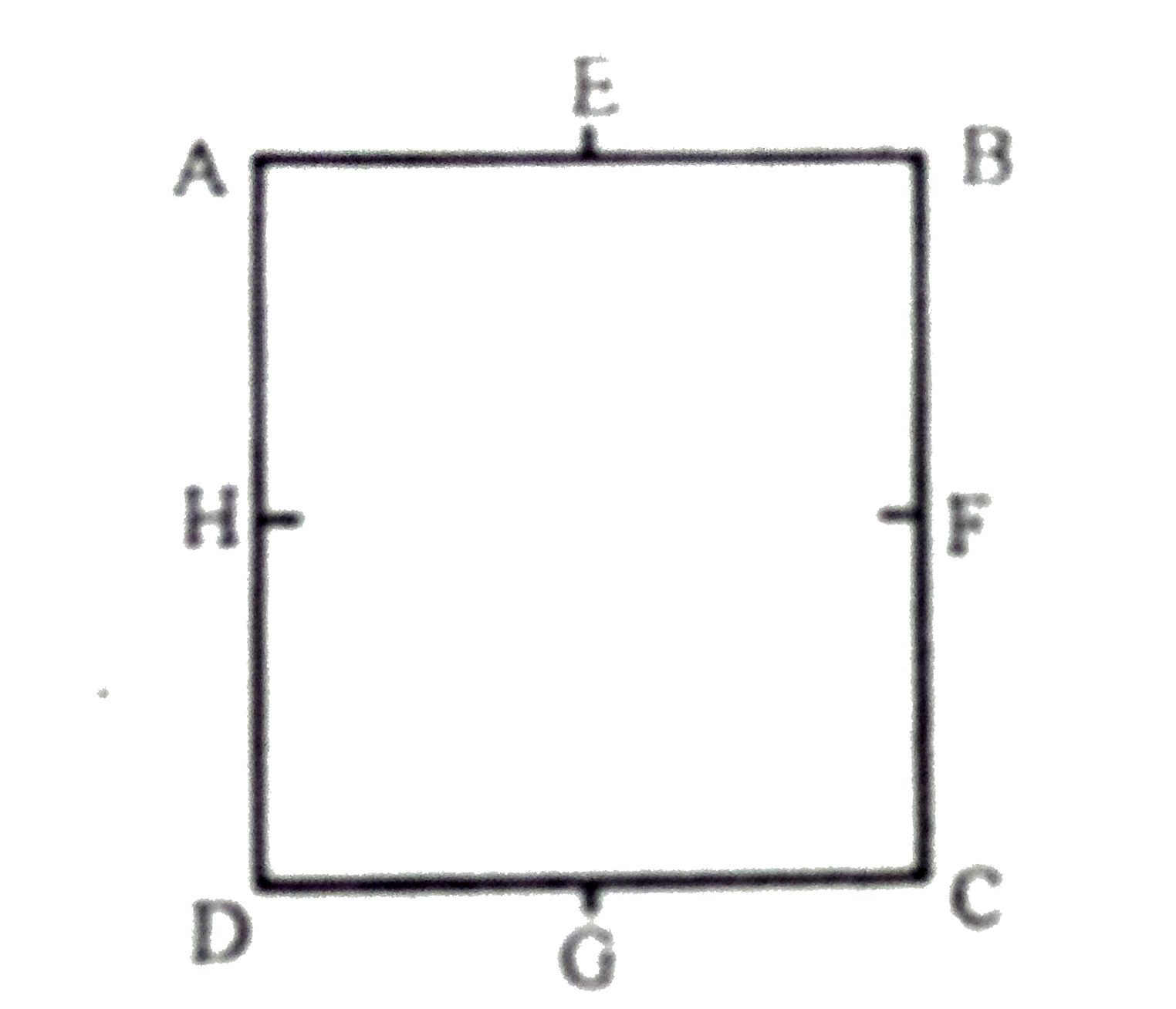
A. EG
B. HF
C. BD
D. BCView SolutionChoose the correct option:
A wire of length l and mass m is first bent in a circle, then in a square and then in an equilateral triangle. The moment of inertia in these three cases about an axis perpendicular to their planes and passing through their centre of mass are I1,I2 and I3 respectively. Then maximum of them isView SolutionA rod of mass 3 kg and of length 3m is bent in the form of an equilateral triangle. The moment of inertia of the triangle about a vertical axis perpendicular to plane and passing through centre of mass is
 View Solution
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 View Solution
View Solution

