A man is standing on a plank which is placed on smooth horizontal surface. There is sufficient friction between feet of man and plank. Now man starts running over plank, correct statement is/are

The cylinder is performing impure rolling motion initially on the plank and finally performs pure rolling motion
The direction of frictional force on the cylinder while rolling on plank is initially in backward direction and finally it attains zero value
The velocity of the centre of mass of the plank + cylinder system, after the cylinder starts pure rolling is √gh2
The minimum length of the plank required for pure rolling of the cylinder over plank is 3v20/16μg, where v0=√2gh.
The correct Answer is:A, B, C, D
As the curve is smooth, there is no gain in angular motion. ⇒mgh=12mu2⇒u=√2gh. i.e., velocity with which it gets onto the plank.
Nμ=12MR2α⇒α=2gμR

Let V and be linear velocity of plank and centre of cylinder when rolling beings.
⇒V=gμ,v=u−gμt,ω=2gμRt And when pure rolling begings.
v−Rω=V⇒u−gμt,ω=2gμRt And when pure rolling begins.
v−Rω=⇒μ−gμt=gμt⇒t=μ4gμ⇒v=3μ4 and V=μ4
⇒ Velocity of centre of mass =m(3μ/4)+m(μ/4)m+m=μ2
For cylinder w.r.t. plank, ar=−2gμ,μr=μ
vr=3u4−μ4=μ2⇒(μ2)2=μ2+2(−2gμ)l⇒l=3μ216gμ.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE MAIN (ARCHIVE)
58 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
26 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (General rigid body motion, Rolling)
10 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA man is running with a constant acceleration on a plank which is placed on a horizontal smooth surface. Then choose the correct option(s):
View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
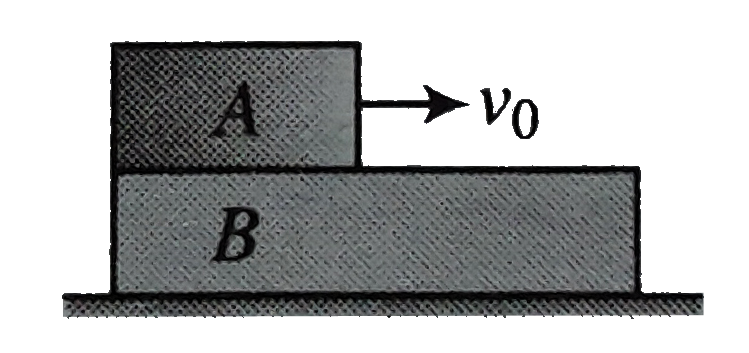
View Solution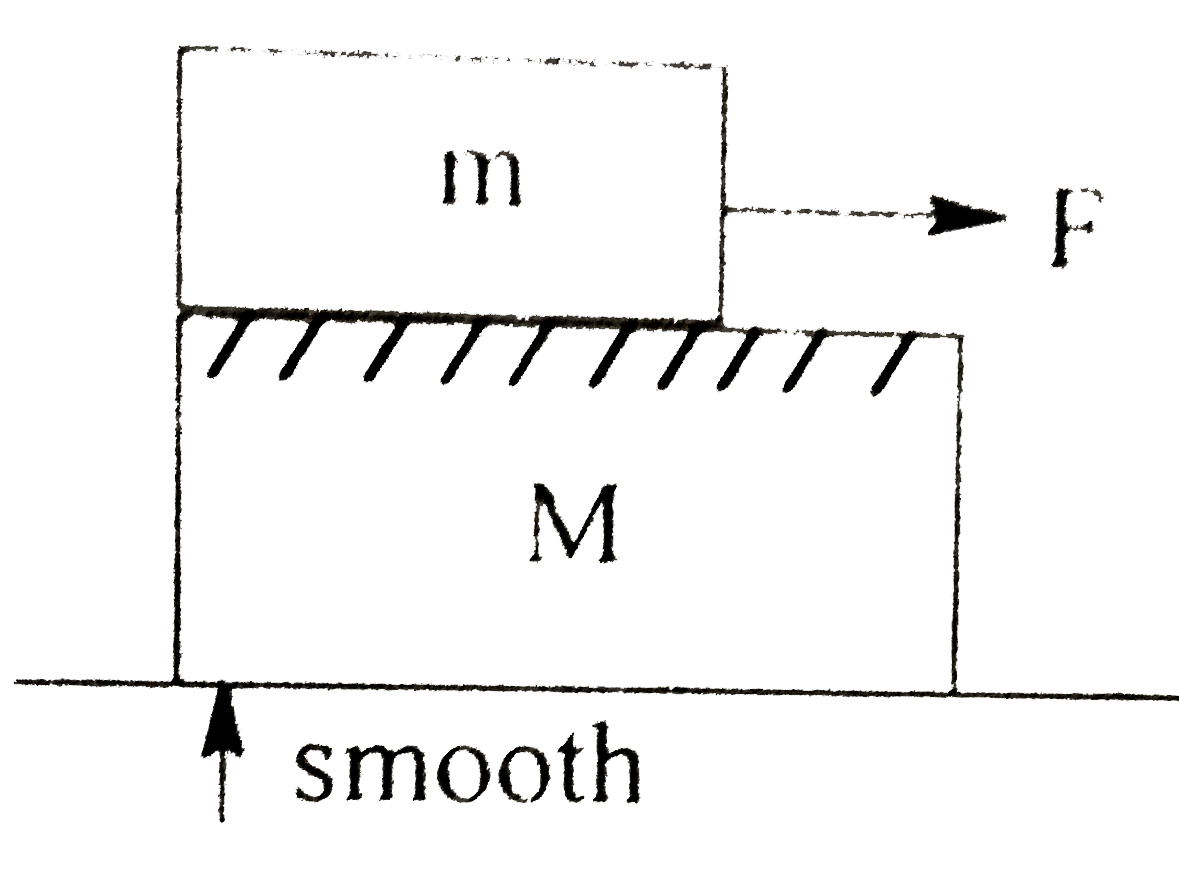
A plank having mass M is placed on smooth horizontal surface. Block of mass m is placed on it coefficient of friction between block and plank is μ0+kx, where k is constant and x is relative displacement between block and plank. A force F is applied on block where F=at, where a=10 t is in second. find t0 when relative motion will occur between block and plank.
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:

View SolutionA bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
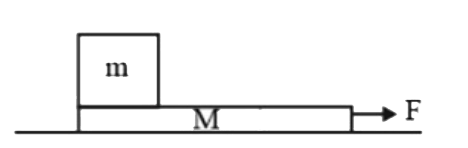
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
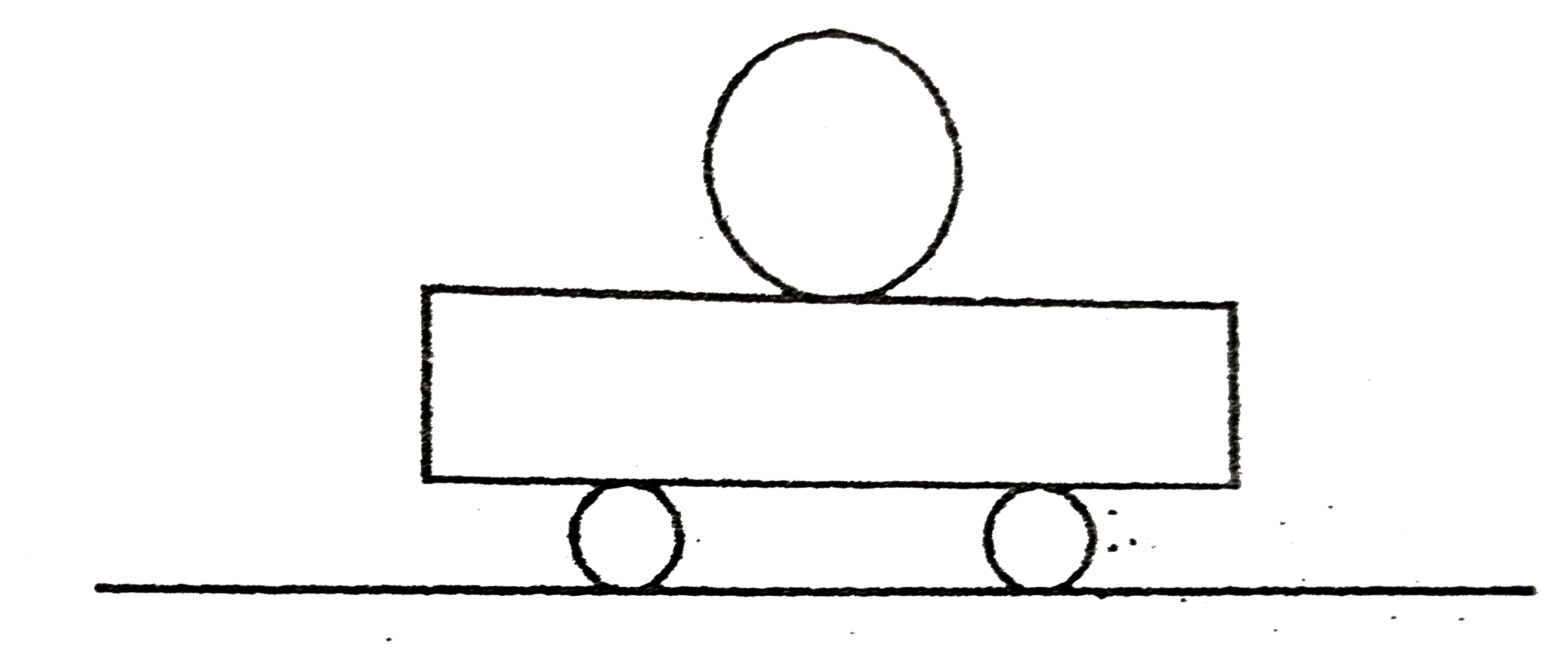
Angular acceleration of sphere is
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping. Force of friction between sphere and plank is

View Solution
