A small bell starts moving from A over a fixed track as shown in the figure . Surface AB is friction from A to B the bell roll ralis without sipping BC is friction , KAKB andKC are kinetic energy of the bell at A,B and C respacecvely.Then
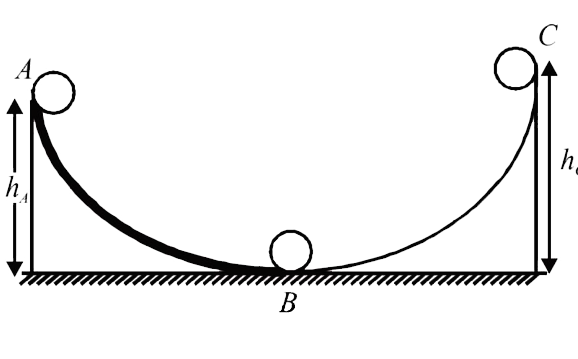
hA>hc,KB>KC
hA>hc,KC>KA
hA=hc,KB=KC
hA<hc,KB>KC
The correct Answer is:A, B
Since work is being done in the process, the sum of kinetic energy, translational kinetic energy, rotational kinetic energy and potential energy will be constant.
KEA+mahA=KEB=KEC+mghC
KEB>KEA and KEB>KEC
Now, if hC>hA, then KEA<KEC.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (LINKED COMPREHENSIVE TYPE)7videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (ASSERTION & REASON TYPE)2videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)26videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions

A ball moves over a fixed track as shown in the figure. From A to B the ball rolls without slipping. If surface BC is frictionless and KA,KB and KC are kinetic energies of the ball at A, B and C respectively then
(a). hA>hC,KB>KC
(b). hA>hC,KC>KA
(c). hA=hC,KB=KC
(d). hA<hC,KB>KCView SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?
 View Solution
View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights B and C ?
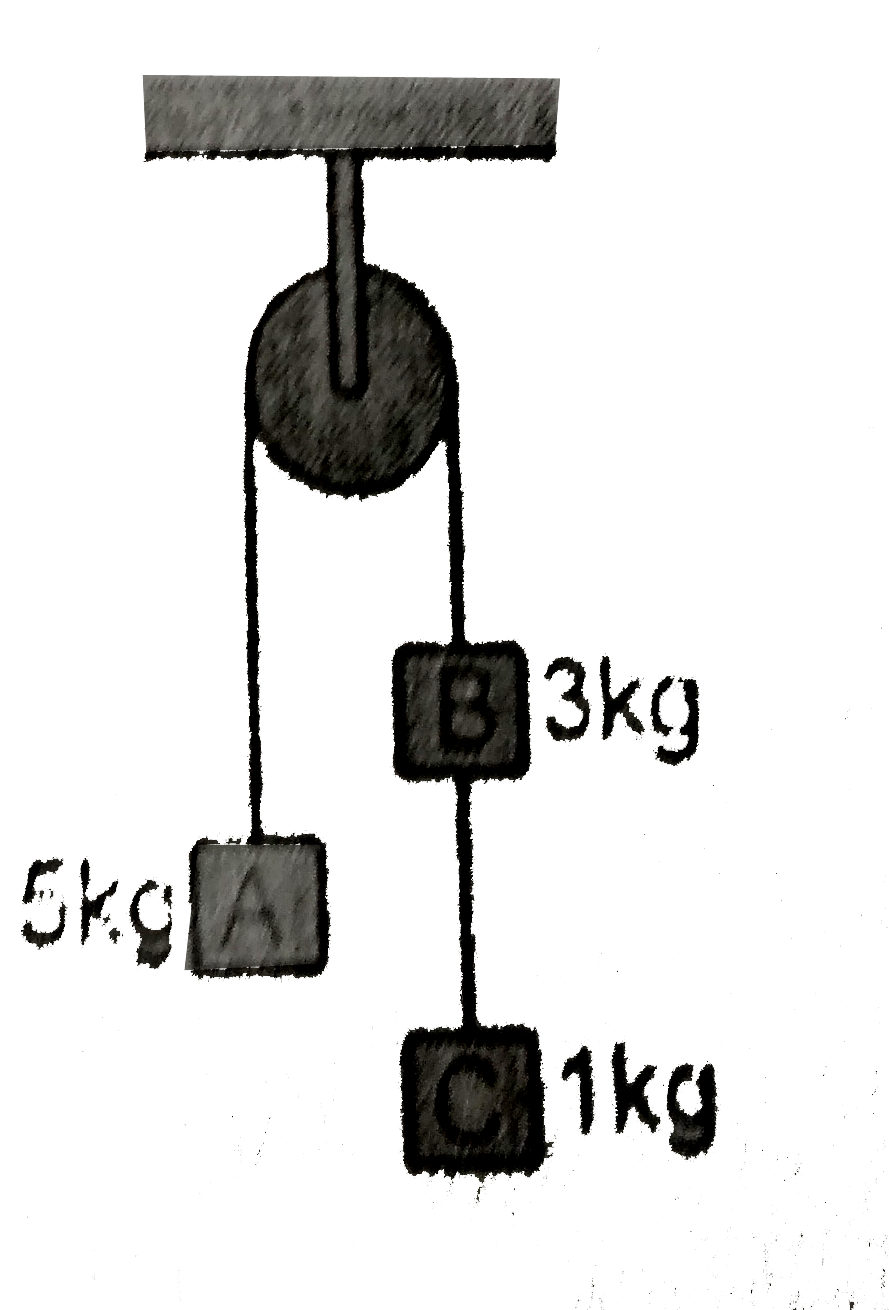 View Solution
View SolutionPortion AB of the wedge shown in figure is rough and BC is smooth. A solid cylinder rolld without slipping from A to B. Find the ratio of translational kinetic energy to rotational kinetic energy, when the cylinder reaches point C.
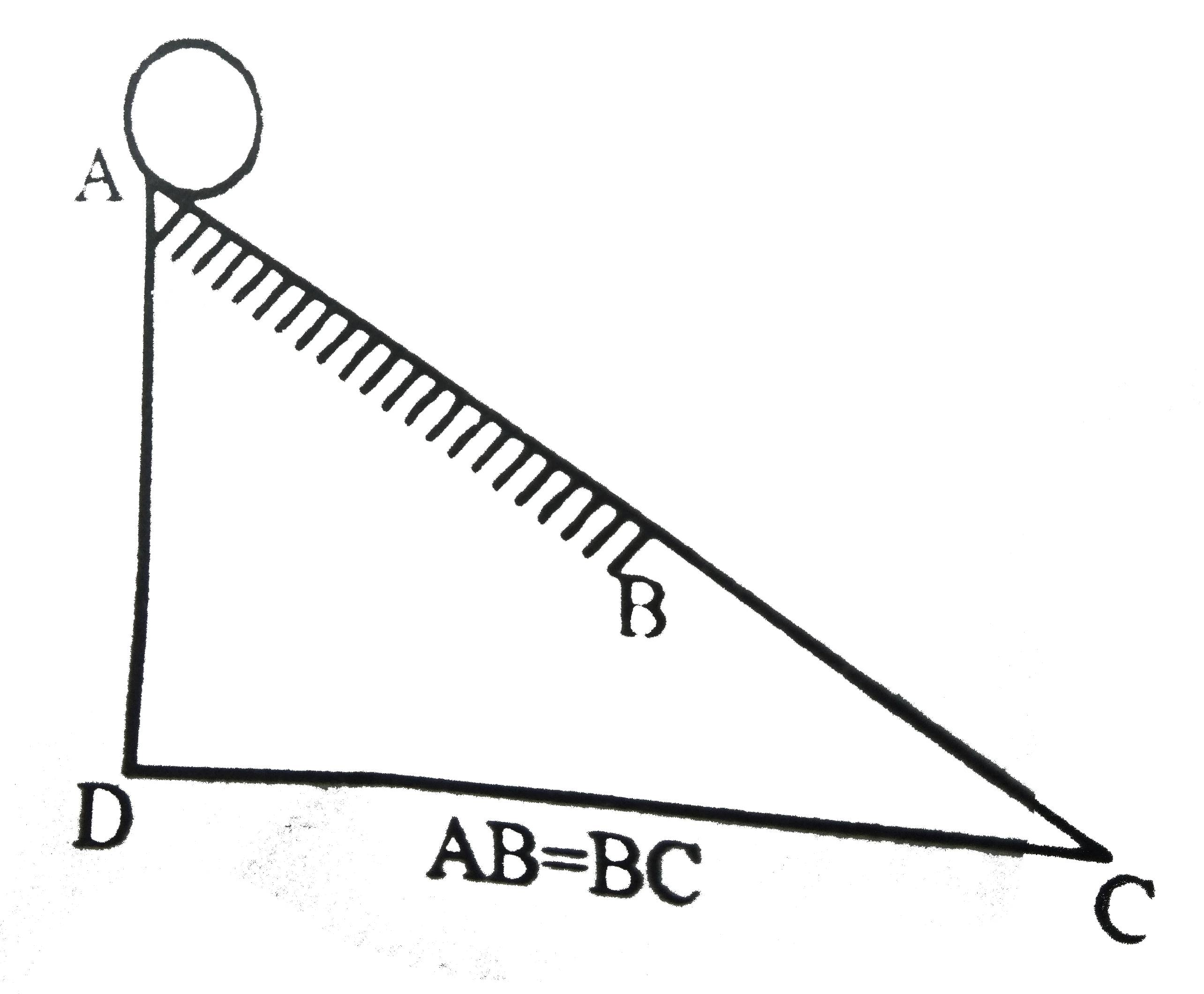 .View Solution
.View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
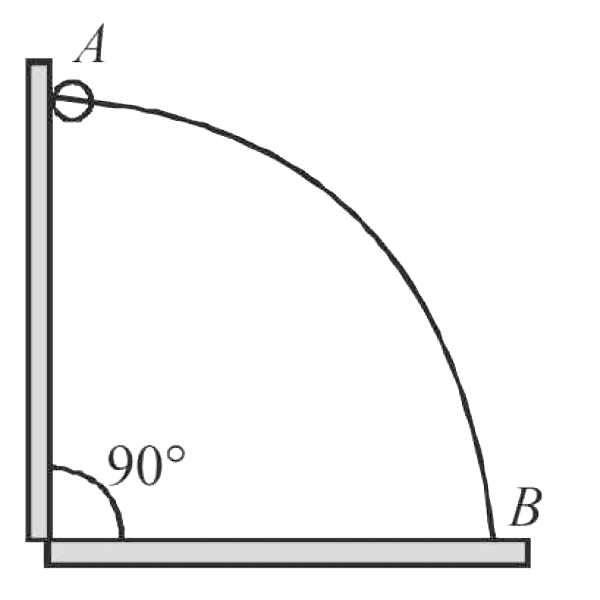 View Solution
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
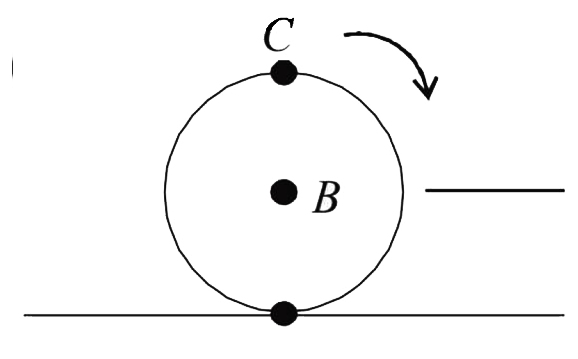 View Solution
View SolutionIn the figure shown, force of friction on A from B will always be right wards
Friction always opposes the relative motion between two bodies in contact.
 View Solution
View SolutionA spherical balll of mass m is the highest point in the space between two fixed , concentic sphere A and B the smaller the two sphere A has a radius R and the space between the two spheres has a width d . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by θ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle θ
(b) Let N_(A)andNBdenote in the magnitubes of the normal reaction force on the bell evered by the sphare A and B repectively Skech the variation of NAandN_(B)asfunctionsofcos theta ∈theran≥0 le theta le pi bydraw∈gtwoseparategraph∈youranswerb∞ktak∈gcos theta an the horizental axas.View SolutionTwo blocks A and B of equal masses are released on two sides of a fixed wedge C as shown in figure. Find the acceleration of centre of mass of blocks A and B. Neglect friction.
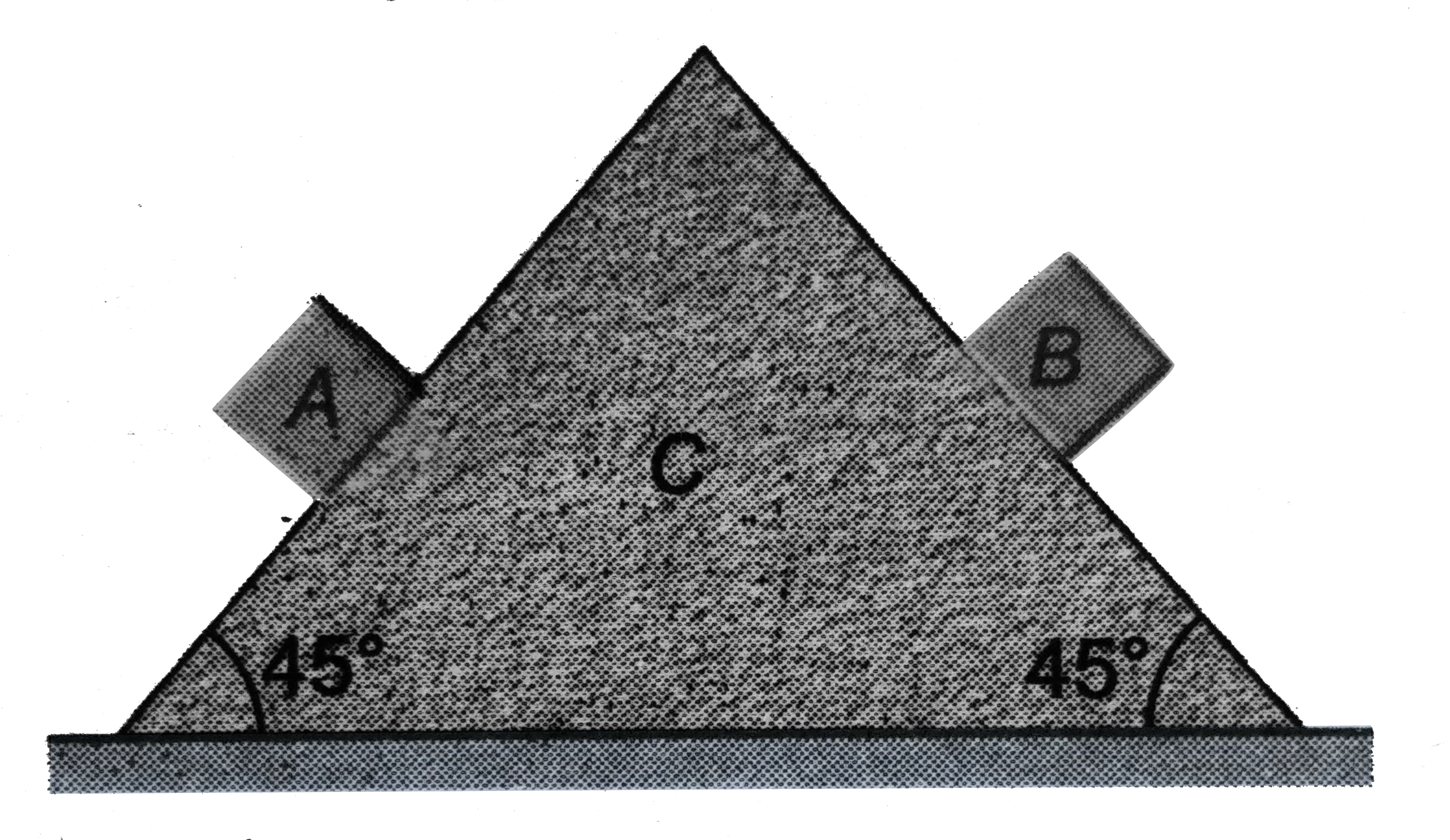 View Solution
View SolutionThree identical solid spheres move down three incline A,B and C are all of the same dimensions. A is without friction, the friction between B and a sphere is sufficient to cause rolling without slipping, the friction between C and a sphere causes rolling with slipping. The kinetic energies, of A,B,C at the bottom of the inclines are EA,EB,EC.
View Solution

