Two charges −q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x(x<<d) perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillation of time period.
T=[8π3∈0md3q2]1/2
![Two charges -q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x (xltltd) perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillation of time period. T = [(8pi^(3) in(0) md^(3))/(q^(2))]^(1//2)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XII_V01_C01_S01_623_Q01.png)
F1=14πe0.Q2(d2+x2)2 [along C to A]…..(i) and F2=14πe0.qq(BC)2=14πe0.qd2+x2………(ii)
Now, resolve the component of .F1andF2
SO net force on q is F=F1cosθ+F2cosθ ,
F=2F1cosθ=2,14πe0.q2(d2+x2).cosθ[∵F1=F2]
In DetlaACO,cosθ=x√d2+x2,F=14πe0=.2q2(d2+x2)3/2
This force is attractive in nature, so =14πe0.2q2.x(d2+x2)3/2
According to question x<<d, so neglect x2 as compared to d2
F=−14πe0.2q2d3.x............(iii) Here F∝−xorF=−ω2x........(iv)
So, the motion is simple harmonic, where ω is the angular frequency. By comparing Equations (iii) and (iv), we get :
ω=√2q24πe0d3morω=2πT
Where, T is the time period of SHM of the charged particle of mass m. T=(8πr3e0md3q2)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )8videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1105videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
Similar Questions
Two equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View SolutionTwo charges q and -3q are placed fixed on x-axis separated by distance d. where should a third charge 2q be placed such that it will not experience any force?
View SolutionTwo charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo charges −q each are separated by distance 2d. A third charge +q is kept at mid-point O. Find potential energy of +q as a function of small distance x from O due to −q charges. Prove that the charge at O is in an unstable equilibrium.
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View SolutionTwo point charges q and −q are separated by a distance 2l. Find the flux strength vector across the circle of radius R placed with its centre coinciding with the of line joining the two charges in the perpendicular plane.
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
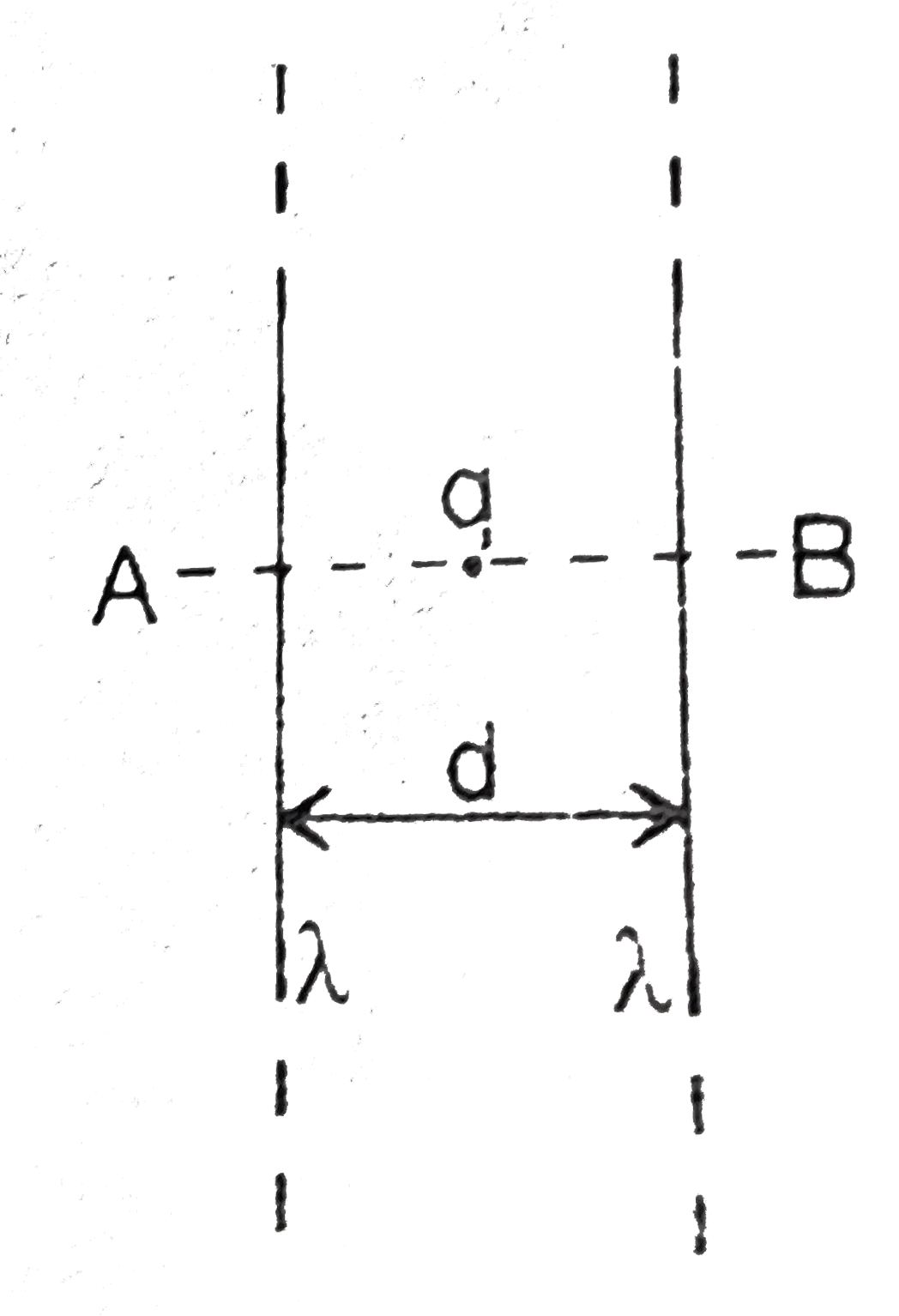 View Solution
View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is
 View Solution
View SolutionTwo points charges +4q and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
View Solution

