A wheel having mass μ has charges +qand−q on diametrically opposite points. It remains in equilibrium on a rough inclined plane in the presence of uniform vertical electric field E =
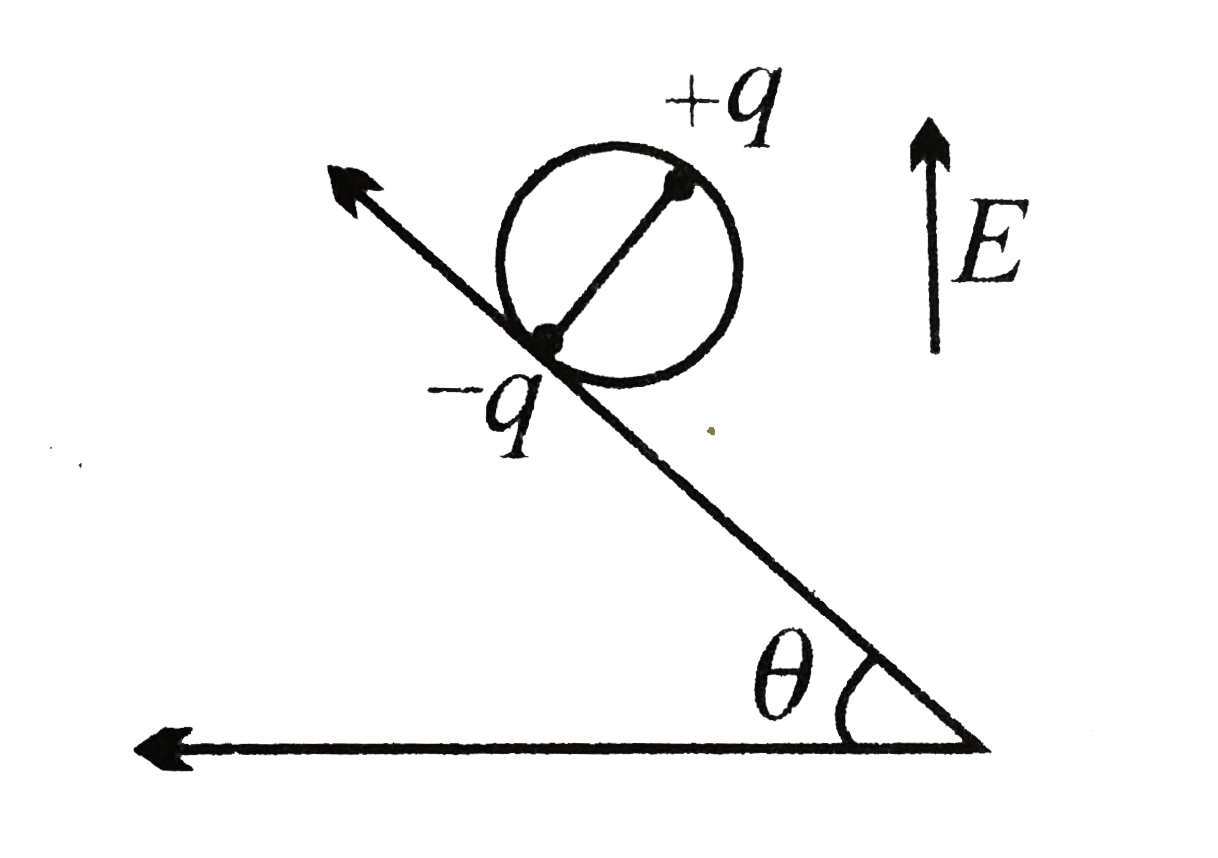
mqq
mg2q
mgtanθ2q
None
The correct Answer is:B
Pe=m gain θR (Balancing torque about point of contact)
E=mq2q
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 260videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN65videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )8videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
Similar Questions
A wheel having mass m has charges +q and −q on diametrically opposite points . It remains in equilibrium on a rough inclined plane in the presence of uniform vertical electric field →E=
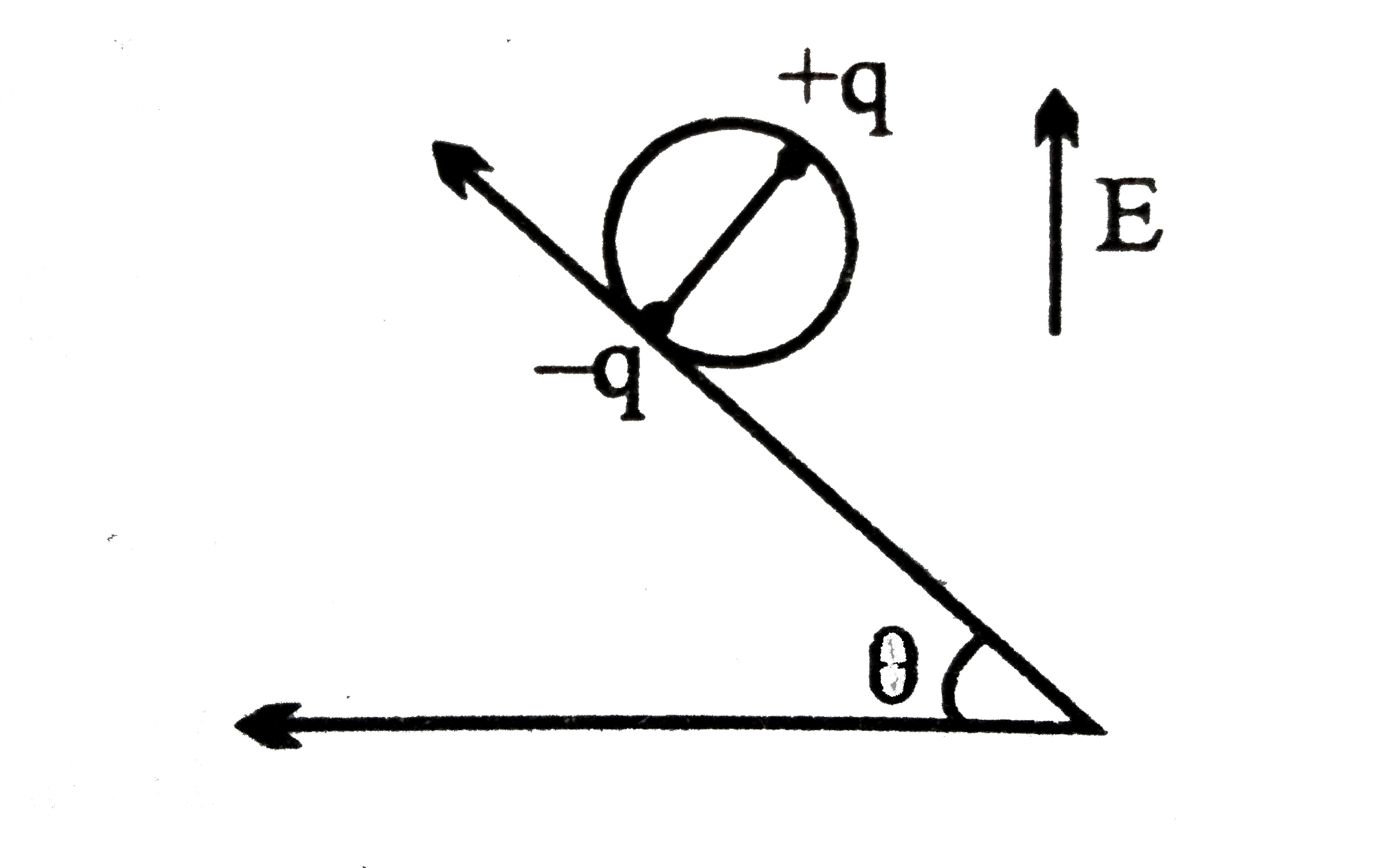.View SolutionTwo point charge +q and -q are fixed on diameterically opposite point on the unirom ring, such that -q is at bottom and is contact will a perfect insulator incline plane. Total mass is equal to m remains in equilibrium on the rough inclined plane in the presence of uniform vertical electric field. Then
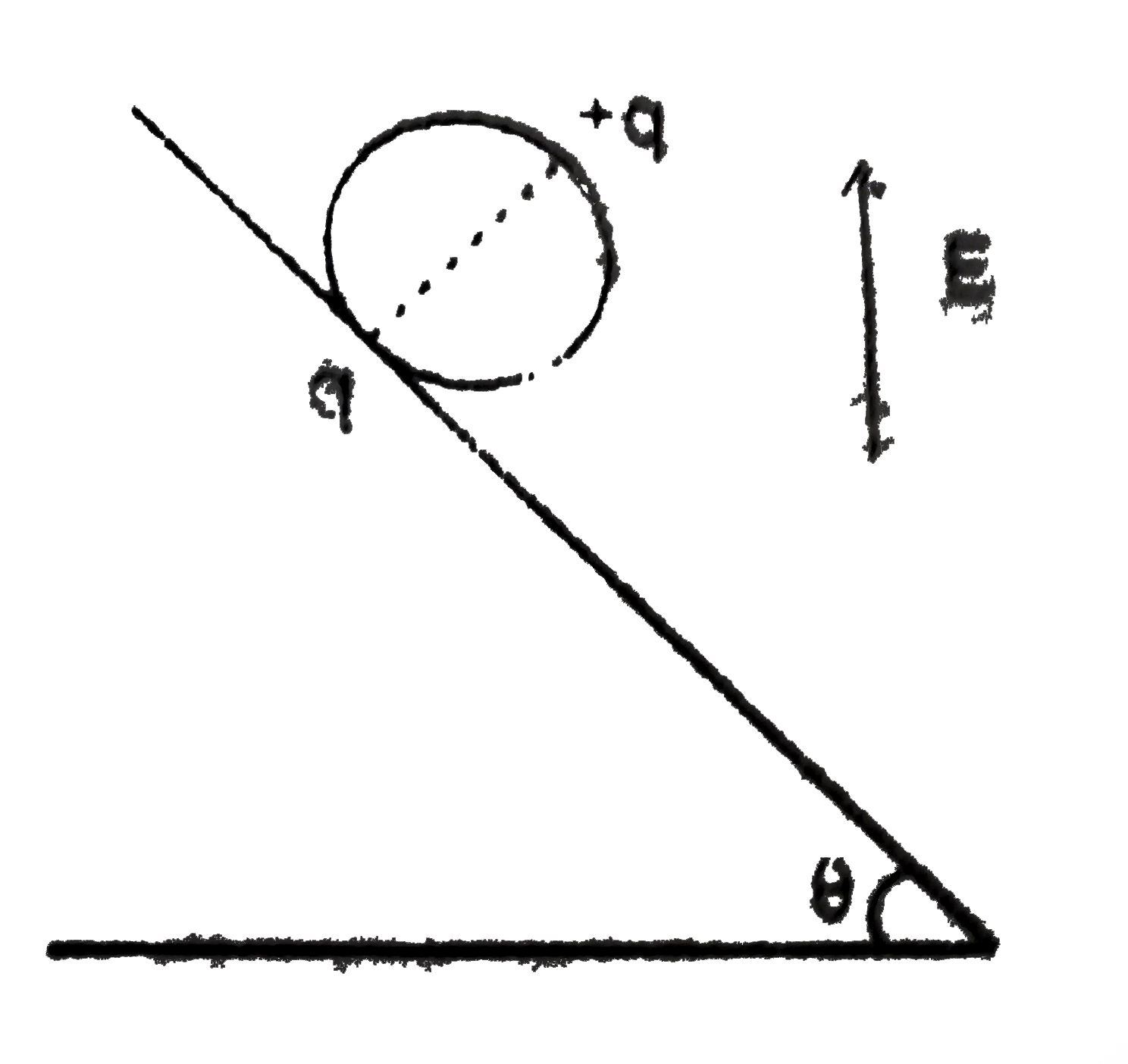View SolutionFind the emf across points P and Q which are diametrically opposite points of a semicircular closed loop moving in a magnetic field as shown in .
View Solutionfind out mass of the charge Q, so that it remains in equilibrium for the given configuration.
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionFind the emf across points P and Q which are diametrically opposite points a semicircular closed loop moving in a magnetic field as shown in . Also draw the electrical equivalence od each branch.
View SolutionFind the emf across points P and Q which are diametrically opposite points a semicircular closed loop moving in a magnetic field as shown in . Also draw the electrical equivalence od each branch.
View SolutionA uniformly charged ring having total charge Q and of radius R is fixed in such a way so that plane of the ring is horizontal. A charged particle of charge q and mass m is in equilibrium at any point lying on y-axis under the combined forces of electric field and earth's gravitational field. Choose the correct statements
View SolutionAn electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged paricle q moving along the axis of the circular wire passes through its centre at speed v. The magnetic force acting on the particle when it passes through the centre has a magnitude
View SolutionAn electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged paricle q moving along the axis of the circular wire passes through its centre at speed v. The magnetic force acting on the particle when it passes through the centre has a magnitude
View Solution