A uniformly charged ring having total charge Q and of radius R is fixed in such a way so that plane of the ring is horizontal. A charged particle of charge q and mass m is in equilibrium at any point lying on y-axis under the combined forces of electric field and earth's gravitational field. Choose the correct statements
The correct Answer is:A, B, C, D
To solve the problem of a charged particle in equilibrium under the influence of the electric field from a uniformly charged ring and the gravitational field, we can follow these steps:
1. Understanding the Setup:
- We have a uniformly charged ring with total charge Q and radius R, fixed in a horizontal plane.
- A charged particle with charge q and mass m is placed along the y-axis (the axis perpendicular to the plane of the ring).
2. Forces Acting on the Charged Particle:
- The gravitational force acting on the particle is Fg=mg (downward).
- The electric force acting on the charged particle due to the ring can be expressed using the electric field E produced by the ring.
3. Electric Field of the Ring:
- The electric field E at a point on the y-axis at a distance y from the center of the ring is given by:
E=14πϵ0⋅Qy(R2+y2)3/2
- This electric field points away from the ring if Q is positive and towards the ring if Q is negative.
4. Equilibrium Condition:
- For the particle to be in equilibrium, the net force acting on it must be zero. Therefore, the upward electric force must balance the downward gravitational force:
Fe=Fg
qE=mg
- Substituting the expression for E:
q⋅14πϵ0⋅Qy(R2+y2)3/2=mg
5. Analyzing the Charge Signs:
- If both Q and q are positive, the electric force will act upward, which means the particle can be in equilibrium above the ring (on the positive y-axis).
- If both Q and q are negative, the electric force will also act upward, allowing equilibrium below the ring (on the negative y-axis).
- If Q and q have opposite signs, the electric force will act downward, which cannot balance the gravitational force acting downward.
6. Specific Charge:
- The specific charge qm can be derived from the equilibrium condition:
qm=g(R2+y2)3/24πϵ0Qy
- This indicates how the charge-to-mass ratio influences the position of equilibrium.
Conclusion:
- The charged particle can be in equilibrium at any point on the y-axis if the conditions regarding the signs of Q and q are satisfied. The specific charge qm determines the nature of the equilibrium.
- We have a uniformly charged ring with total charge Q and radius R, fixed in a horizontal plane.
- A charged particle with charge q and mass m is placed along the y-axis (the axis perpendicular to the plane of the ring).
- The gravitational force acting on the particle is Fg=mg (downward).
- The electric force acting on the charged particle due to the ring can be expressed using the electric field E produced by the ring.
- The electric field E at a point on the y-axis at a distance y from the center of the ring is given by:
E=14πϵ0⋅Qy(R2+y2)3/2
- This electric field points away from the ring if Q is positive and towards the ring if Q is negative.
- For the particle to be in equilibrium, the net force acting on it must be zero. Therefore, the upward electric force must balance the downward gravitational force:
Fe=Fg
qE=mg
- Substituting the expression for E:
q⋅14πϵ0⋅Qy(R2+y2)3/2=mg
- If both Q and q are positive, the electric force will act upward, which means the particle can be in equilibrium above the ring (on the positive y-axis).
- If both Q and q are negative, the electric force will also act upward, allowing equilibrium below the ring (on the negative y-axis).
- If Q and q have opposite signs, the electric force will act downward, which cannot balance the gravitational force acting downward.
- The specific charge qm can be derived from the equilibrium condition:
qm=g(R2+y2)3/24πϵ0Qy
- This indicates how the charge-to-mass ratio influences the position of equilibrium.
- The charged particle can be in equilibrium at any point on the y-axis if the conditions regarding the signs of Q and q are satisfied. The specific charge qm determines the nature of the equilibrium.
Similar Questions
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View SolutionA Circular ring of radius 3a is uniformly charged with charge q is kept in x−y plane with center at origin. A particle of charge q and mass m is projected frim x=4 towards origin. Find the minimum speed of projection such that it reaches origin.
_2019_CBT5_E01_042_Q01.png) View Solution
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
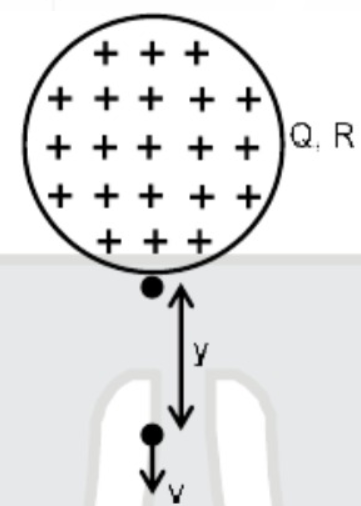 View Solution
View SolutionFor a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionA charge particle q is projected in an electric field produced by a fixed point charge Q as shown in figure. Mark the correct statements.
 View Solution
View SolutionIn a uniformly charged sphere of total charge Q and radius R, the electric field E is plotted as function of distance from the centre, The graph which would correspond to the above will be:
View SolutionConsider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
View SolutionA uniformly charged ring of radius R is rotated about its axis with constant linear speed v of each of its particle. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from centre of ring is (c is speed of light )
 View Solution
View SolutionA charged particle having charge q is moving in a uniform magnetic field B parallel to the lines of field force, the magnetic force acting on a charge will be qvB
View Solution

