The potential in the electric field varies as V=−ax2+b with respect to x - coordinate, where a and b are constants. Find the charge density ρ(x) in a space.
−6aε0r
−24πaε0
−6aε0
−24πaε0r
The correct Answer is:C
Electric field E=−dϕdr=−2ar
By Gauss theorem E(4πr2)=qe0⇒q=−8πe0ar3
p=dqdV=dqdr×drdV=(−24πe0ar2)(14πr2)=−6e0a
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
Similar Questions
The electric potential in a region is given as V=−4ar2+3b, where r is distance from the origin, a and b are constants. If the volume charge density in the region is given by ρ=naε0, then what is the value of n?
View SolutionThe field potentail in a certain region of space depends only on the x coordinate as φ=−ax2+b, where a and b are constants. Find the distribution of the space charge ρ(x).
View SolutionFind the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
View SolutionThe potential energy of a particle varies with distance x from a fixed origin as V=A√XX+B where A and B are constants . The dimension of AB are
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionDetermine the electric field strength vector if the potential of this field depends on X, coordinates as V = 10 axy
View SolutionFind the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
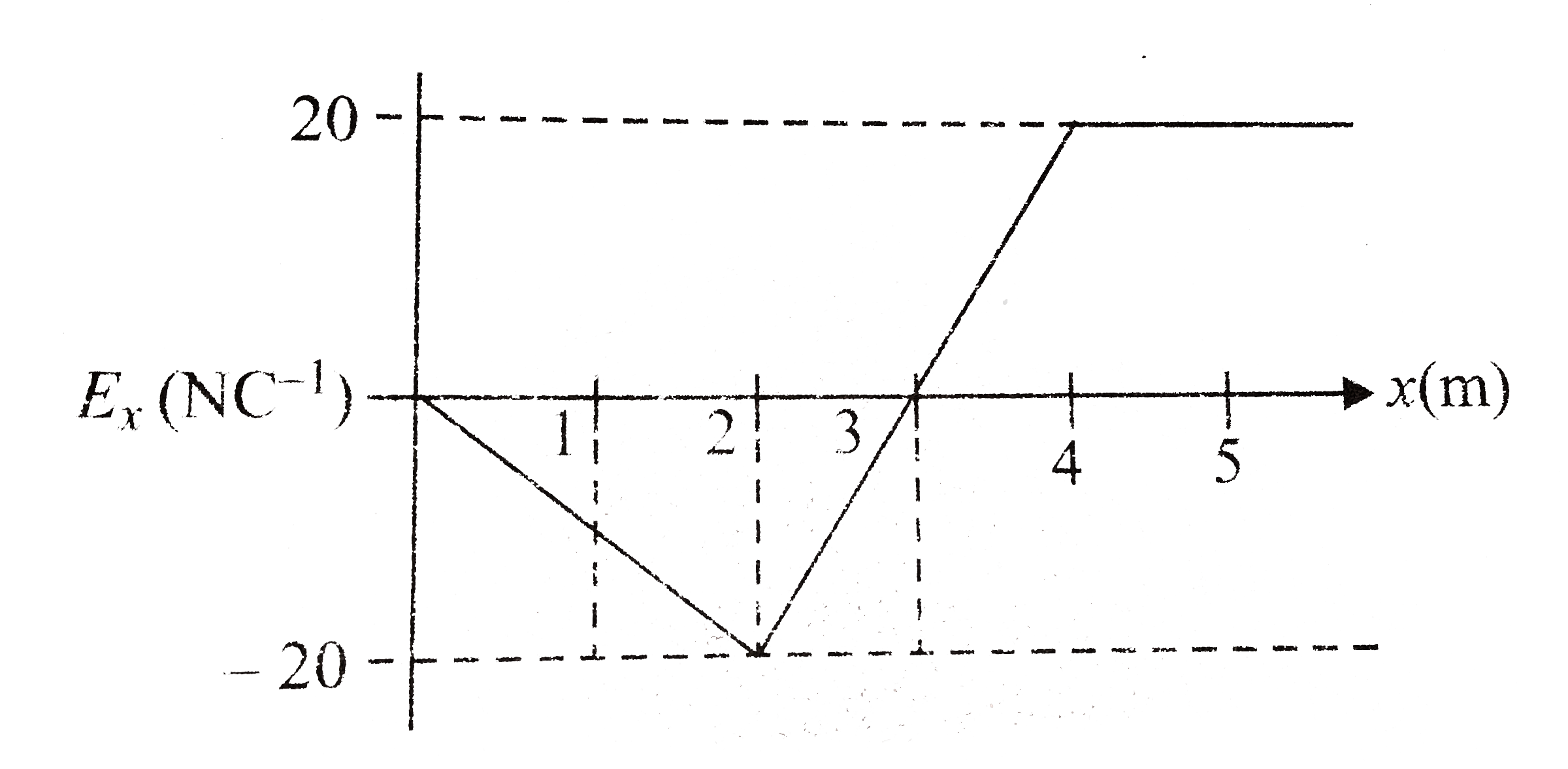
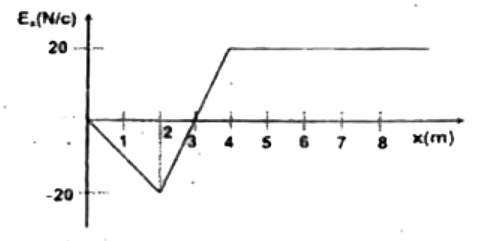
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
View SolutionA partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates xasU(x)=Ax2−Bx where A and B are positive constant.
Find the time period of small oscillation that the partical perform about equilibrium possition.
View Solution