For a reaction of reversible nature, net rate is (dxdt)=k1[A][B]−k2[C] hence, given reaction is :
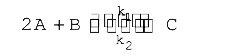
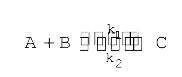

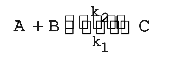
The correct Answer is:B
To solve the problem, we need to analyze the given net rate equation for a reversible reaction and identify the correct form of the reaction based on the provided options.
1. Understanding the Net Rate Equation:
The net rate of a reversible reaction is given by:
dxdt=k1(A)(B)−k2(C)
Here, k1 is the rate constant for the forward reaction, and k2 is the rate constant for the backward reaction.
2. Identifying the Forward and Backward Reactions:
- The forward reaction can be represented as:
A+B⇌C
- The rate of the forward reaction is proportional to the concentrations of the reactants:
Rforward=k1(A)(B)
- The rate of the backward reaction is proportional to the concentration of the product:
Rbackward=k2(C)
3. Formulating the Net Rate:
The net rate of the reaction can be expressed as:
Net Rate=Rforward−Rbackward=k1(A)(B)−k2(C)
This matches the given equation.
4. Analyzing the Options:
- We need to check each option provided to see which one matches the derived net rate equation.
- The correct option should have the form k1(A)(B)−k2(C).
5. Conclusion:
After checking the options, we find that the option which states:
Rforward=k1(A)(B)andRbackward=k2(C)
matches the derived net rate equation. Therefore, the correct answer is option B.
The net rate of a reversible reaction is given by:
dxdt=k1(A)(B)−k2(C)
Here, k1 is the rate constant for the forward reaction, and k2 is the rate constant for the backward reaction.
- The forward reaction can be represented as:
A+B⇌C
- The rate of the forward reaction is proportional to the concentrations of the reactants:
Rforward=k1(A)(B)
- The rate of the backward reaction is proportional to the concentration of the product:
Rbackward=k2(C)
The net rate of the reaction can be expressed as:
Net Rate=Rforward−Rbackward=k1(A)(B)−k2(C)
This matches the given equation.
- We need to check each option provided to see which one matches the derived net rate equation.
- The correct option should have the form k1(A)(B)−k2(C).
After checking the options, we find that the option which states:
Rforward=k1(A)(B)andRbackward=k2(C)
matches the derived net rate equation. Therefore, the correct answer is option B.
Topper's Solved these Questions
- CHEMICAL KINETICS Book:VMC MODULES ENGLISHChapter:CHEMICAL KINETICS Exercise:Level-2 ( Numerical Value Type for JEE Main )
Explore 15 Videos
- CHEMICAL KINETICS Book:VMC MODULES ENGLISHChapter:CHEMICAL KINETICS Exercise:JEE Main (Archive)
Explore 56 Videos
- CHEMICAL KINETICS Book:VMC MODULES ENGLISHChapter:CHEMICAL KINETICS Exercise:Level-1
Explore 75 Videos
- CHEMICAL EQUILIBRIUMBook:VMC MODULES ENGLISHChapter:CHEMICAL EQUILIBRIUMExercise:IN-CHAPTER EXERCISE - G
Explore 10 Videos
- CHEMICAL THERMODYNAMICS Book:VMC MODULES ENGLISHChapter:CHEMICAL THERMODYNAMICS Exercise:IN - CHAPTER EXERCISE - L
Explore 10 Videos
Similar Questions
Knowledge Check
The rate of certain hypothetical reaction
A+B+C→ Products, is given by
r=−dAdt=k[A]1/2[B]1/3[C]1/4
The order of a reaction is given byA1B2C13/12D5/4
For a reaction, A+2B→C, rate is given by +d[C]dt=k[A][B], hence, the order of the reaction is
View SolutionThe rate of the reaction A+B+C→ Product is given by: rate =−d[A]dt=k[A]1/2[B]1/4[C]0 The order of reaction is:
View SolutionFor a reaction A+B→ Products, the rate law is -Rate =k[A][B]3/2
Can the reaction be an elementray reaction ? Explain.
View SolutionIf the rate of reaction between A and B is given by rate =k[A][B]2, then the reaction is
View Solution(a) For a reaction AB→P , the rate law is given by, r=k[A]1/2[B]2. What is the order of this reaction?
(b) A first order reaction is found to have a rate constant k=5.5×10−14s−1, Find the half life of the reaction.
View SolutionThe rate of certain hypothetical reaction
A+B+C→ Products, is given by
r=−dAdt=k[A]1/2[B]1/3[C]1/4
The order of a reaction is given by
View SolutionThe rate constant for a forward reaction in a reversible reaction (Keq=106) is 102 . Calculate rate constant for its backward reaction
View Solution
