The following data were obtained at a certain temperature for the decomposition of ammonia in contact with tungsten:
p (m m Hg) 50 100 200
Relative t1/2 3.64 1.82 0.91
Find the order of the reaction.
To determine the order of the reaction for the decomposition of ammonia in contact with tungsten, we will use the relationship between the half-life of the reaction and the pressure of the reactant. The provided data includes the pressure (in mm Hg) and the corresponding relative half-lives.
Given Data:
- Pressure (P) in mm Hg: 50, 100, 200
- Relative half-life (t₁/₂): 3.64, 1.82, 0.91
1. Understanding the Relationship:
The half-life (t₁/₂) of a reaction is related to the pressure (P) by the formula:
t1/2∝1Pn−1
This implies that:
t1/2⋅Pn−1=k
where k is a constant.
2. Setting Up Ratios:
We will take two sets of data points to form a ratio. Let's use the first two data points (P₁ = 50 mm Hg, t₁/₂₁ = 3.64) and (P₂ = 100 mm Hg, t₁/₂₂ = 1.82):
t1/21t1/22=Pn−12Pn−11
3. Substituting Values:
Substitute the values into the equation:
3.641.82=100n−150n−1
4. Simplifying the Left Side:
Calculate the left side:
3.641.82=2
5. Simplifying the Right Side:
The right side simplifies as follows:
100n−150n−1=(10050)n−1=2n−1
6. Setting the Equation:
Now we have:
2=2n−1
7. Solving for n:
Since the bases are the same, we can equate the exponents:
1=n−1
Thus, solving for n gives:
n=2
Conclusion:
The order of the reaction is 2.
- Pressure (P) in mm Hg: 50, 100, 200
- Relative half-life (t₁/₂): 3.64, 1.82, 0.91
The half-life (t₁/₂) of a reaction is related to the pressure (P) by the formula:
t1/2∝1Pn−1
This implies that:
t1/2⋅Pn−1=k
where k is a constant.
We will take two sets of data points to form a ratio. Let's use the first two data points (P₁ = 50 mm Hg, t₁/₂₁ = 3.64) and (P₂ = 100 mm Hg, t₁/₂₂ = 1.82):
t1/21t1/22=Pn−12Pn−11
Substitute the values into the equation:
3.641.82=100n−150n−1
Calculate the left side:
3.641.82=2
The right side simplifies as follows:
100n−150n−1=(10050)n−1=2n−1
Now we have:
2=2n−1
Since the bases are the same, we can equate the exponents:
1=n−1
Thus, solving for n gives:
n=2
The order of the reaction is 2.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Main (Archive)56videos
CHEMICAL KINETICS
- BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Advanced (Archive)52videos
CHEMICAL KINETICS
- BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-250videos
CHEMICAL KINETICS
- BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - IN-CHAPTER EXERCISE - G10videos
CHEMICAL EQUILIBRIUM
- BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - L10videos
CHEMICAL THERMODYNAMICS
Similar Questions
The following data were obtained at a certain temperature for the decomposition of NH3 in contact with catalyst.
P(mn)2550t1/21.820.91
The order of reaction isView SolutionFollowing data were obtained for the catalytic decomposition of ammonia :
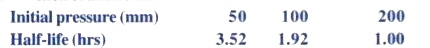
Find the order of reaction.View SolutionFollowing data were obtained for the catalytic decomposition of ammonia :
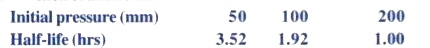
Find the order of reaction.View SolutionFollowing data were obtained for the catalytic decomposition of ammonia :
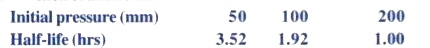
Find the order of reaction.View SolutionIn the decomposition of Ammonia it was found that at 50 torr pressure t(1/2) was 3.64 hour while at 100 torr t(1/2) was 1.82 hours. Then order of reaction would be:
View SolutionIn te decomposition of Ammonia it was found that at 50 torr pressure t(1/2) was 3.64 hour while at 100 torr t(1/2) was 1.82 hours. Then order of reaction would be:
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
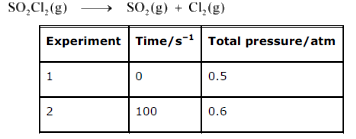
Calculate the rate of the reaction when total pressure is 0.65 atmView SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
SO2Cl2(g)→SO2(g)+Cl2(g)

What is the rate of reaction when total pressure of 0.65 atm?View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at constant volume :
ExperimentTime (s)Total Pressure (atm)100.321000.5
Calculate rate constant
[Given : log 6 = 0.7782, log 3 = 0.4771]View SolutionFor the decompoistion of HI at 1000K(2HI→H2+I2), following data were obtained:
∣∣ ∣ ∣ ∣ ∣∣[HI](M)Rate of decomposition of HI(molL−1s−1)0.12.75×10−80.211×10−80.324.75×10−8∣∣ ∣ ∣ ∣ ∣∣
The order of reaction isView Solution

