For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t ae P0andPt respectively. Initially, only A is present with concentration [A]0andt1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct options (s) is (are) :
(Assume that all these behave as ideal gases)
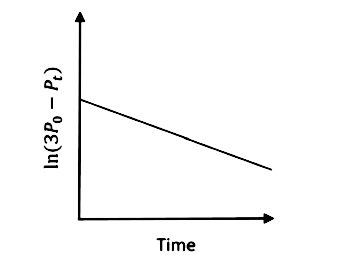
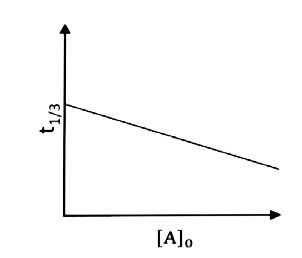
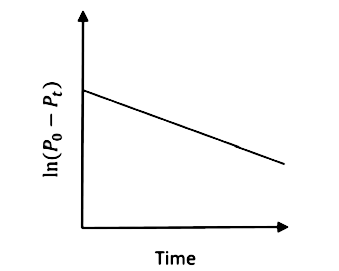
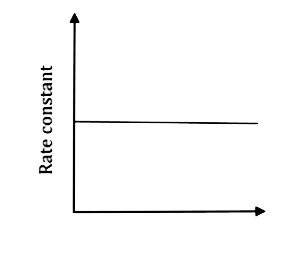
The correct Answer is:A, D
To solve the problem, we will analyze the first-order reaction given and derive the necessary relationships step by step.
Step 1: Understand the Reaction
The reaction is given as:
A(g)→2B(g)+C(g)
Initially, only A is present with an initial pressure P0.
Step 2: Define Initial Conditions
At t=0:
- Partial pressure of A, PA(0)=P0
- Partial pressures of B and C are both 0.
Step 3: Define Conditions at Time t
At time t:
- Let x be the change in pressure due to the reaction.
- The partial pressure of A will be PA(t)=P0−x.
- The partial pressure of B will be PB(t)=2x (since 2 moles of B are produced).
- The partial pressure of C will be PC(t)=x.
Step 4: Total Pressure at Time t
The total pressure at time t is given by:
Pt=PA(t)+PB(t)+PC(t)=(P0−x)+2x+x=P0+2x
Step 5: Condition for t1/3
The time t1/3 is defined as the time required for the partial pressure of A to reach 13P0:
PA(t1/3)=P0−x=13P0
From this, we can find x:
P0−x=13P0
x=P0−13P0=23P0
Step 6: Substitute x into Total Pressure Equation
Substituting x into the total pressure equation:
Pt=P0+2x=P0+2(23P0)=P0+43P0=73P0
Step 7: Relate to Rate Constant
For a first-order reaction, the rate constant k can be expressed as:
k=1tln(P0P0−x)
Using x=23P0:
k=1t1/3ln⎛⎝P013P0⎞⎠=1t1/3ln(3)
Step 8: Conclusion
The options that do not depend on concentration are correct. The correct options are those that reflect the derived relationships, specifically those that are constants and do not vary with concentration.
The reaction is given as:
A(g)→2B(g)+C(g)
Initially, only A is present with an initial pressure P0.
At t=0:
- Partial pressure of A, PA(0)=P0
- Partial pressures of B and C are both 0.
At time t:
- Let x be the change in pressure due to the reaction.
- The partial pressure of A will be PA(t)=P0−x.
- The partial pressure of B will be PB(t)=2x (since 2 moles of B are produced).
- The partial pressure of C will be PC(t)=x.
The total pressure at time t is given by:
Pt=PA(t)+PB(t)+PC(t)=(P0−x)+2x+x=P0+2x
The time t1/3 is defined as the time required for the partial pressure of A to reach 13P0:
PA(t1/3)=P0−x=13P0
From this, we can find x:
P0−x=13P0
x=P0−13P0=23P0
Substituting x into the total pressure equation:
Pt=P0+2x=P0+2(23P0)=P0+43P0=73P0
For a first-order reaction, the rate constant k can be expressed as:
k=1tln(P0P0−x)
Using x=23P0:
k=1t1/3ln⎛⎝P013P0⎞⎠=1t1/3ln(3)
The options that do not depend on concentration are correct. The correct options are those that reflect the derived relationships, specifically those that are constants and do not vary with concentration.
Topper's Solved these Questions
- CHEMICAL KINETICS Book:VMC MODULES ENGLISHChapter:CHEMICAL KINETICS Exercise:JEE Main (Archive)
Explore 56 Videos
- CHEMICAL EQUILIBRIUMBook:VMC MODULES ENGLISHChapter:CHEMICAL EQUILIBRIUMExercise:IN-CHAPTER EXERCISE - G
Explore 10 Videos
- CHEMICAL THERMODYNAMICS Book:VMC MODULES ENGLISHChapter:CHEMICAL THERMODYNAMICS Exercise:IN - CHAPTER EXERCISE - L
Explore 10 Videos
Similar Questions
For a first order gas phase reaction :
A(g)→2B(g)+C(g)
P0 be initial pressure of A and Pt the total pressure at time 't'. Integrated rate equation is :
View SolutionFor the first order reaction A(g)→2B(g)+C(g), the initial pressure is PA=90mHg, the pressure after 10 minutes is found to be 180mmHg. The rate constant of the reaction is
View SolutionHeat of reaction A(s)+B(g)→2C(g) is 40 kJ at 300 K and constant volume. Hence, heat of reaction at constant pressure and at 300 K is,
View SolutionKp for the reaction A⇔B is 4. If initially only A is present then what will be the partial pressure of B after equilibrium ?
View SolutionFor a first order homogeneous gaseous reaction
A→2B+C
if the total pressure after time t was P1 and after long time (t→∞) was P∞ then K in terms of Pt1 P∞ t is
View SolutionThe reaction A(g) + 2B(g) → C(g) is an elementary reaction. In an experiment involving this reaction, the initial pressures of A and B are PA = 0.40 atm and PB = 1.0 atm respectively. When PC=0.3 atm, the rate of the reaction relative to the initial rate is:-
View SolutionFor a first order homogenous gaseous reaction, A→2B+C
then initial pressure was Pi while total pressure after time 't' was Pt. The right expression for the rate constants k in terms of Pi,Pt and t is :
View SolutionThe reaction A(g)→B(g)+2C(g) is a first-order reaction with a rate constant of 2.303×10−3s−1. Strating with 0.1 moles of 'A' in a 2 litre vessel, find the concentration of A after 301 sec when the reaction is allowed to take place at constant pressure at 300 K.
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View Solution