The X and Y components of a force F acting at 30∘ to x-axis are respectively :
F√2,F
F2,√32F
√32F,12F
F,F√2
The correct Answer is:C
To find the X and Y components of a force F acting at an angle of 30∘ to the x-axis, we can follow these steps:
Step 1: Understand the Force Components
The force F can be resolved into two components:
- The X component, which lies along the x-axis.
- The Y component, which lies along the y-axis.
Step 2: Use Trigonometric Functions
The components can be calculated using trigonometric functions:
- The X component is given by:
Fx=Fcos(30∘)
- The Y component is given by:
Fy=Fsin(30∘)
Step 3: Calculate the X Component
Now, we need to calculate Fx:
- We know that cos(30∘)=√32.
- Therefore, substituting this value, we get:
Fx=Fcos(30∘)=F⋅√32=√32F
Step 4: Calculate the Y Component
Next, we calculate Fy:
- We know that sin(30∘)=12.
- Therefore, substituting this value, we get:
Fy=Fsin(30∘)=F⋅12=12F
Step 5: Final Results
Thus, the components of the force F acting at 30∘ to the x-axis are:
- X component: Fx=√32F
- Y component: Fy=12F
Conclusion
The X and Y components of the force F are respectively √32F and 12F.
---
The force F can be resolved into two components:
- The X component, which lies along the x-axis.
- The Y component, which lies along the y-axis.
The components can be calculated using trigonometric functions:
- The X component is given by:
Fx=Fcos(30∘)
- The Y component is given by:
Fy=Fsin(30∘)
Now, we need to calculate Fx:
- We know that cos(30∘)=√32.
- Therefore, substituting this value, we get:
Fx=Fcos(30∘)=F⋅√32=√32F
Next, we calculate Fy:
- We know that sin(30∘)=12.
- Therefore, substituting this value, we get:
Fy=Fsin(30∘)=F⋅12=12F
Thus, the components of the force F acting at 30∘ to the x-axis are:
- X component: Fx=√32F
- Y component: Fy=12F
The X and Y components of the force F are respectively √32F and 12F.
Topper's Solved these Questions
Similar Questions
The vertical component of a force acting at 60∘ to the horizontal is 8.48 N . Find the force and the horizontal component .
View SolutionThe x and y components of a vector are 4√3m and 4 m respectively. What angle does the vector make with positive x-axis ?
View SolutionThe x and y-components of vector A are 4 m and 6 m respectively. The x and y-components of vector A + B are 10 m and 9 m respectively. Calculate for the vector B the following:
(a) its x and y-components
(b) its length
(c ) the angle it makes with x-axis.
View SolutionMaximum and minimum values of the resultant of two forces acting at a point are 7 N and 3N respectively. The smaller force will be equal to x N. Find x
View SolutionThree components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
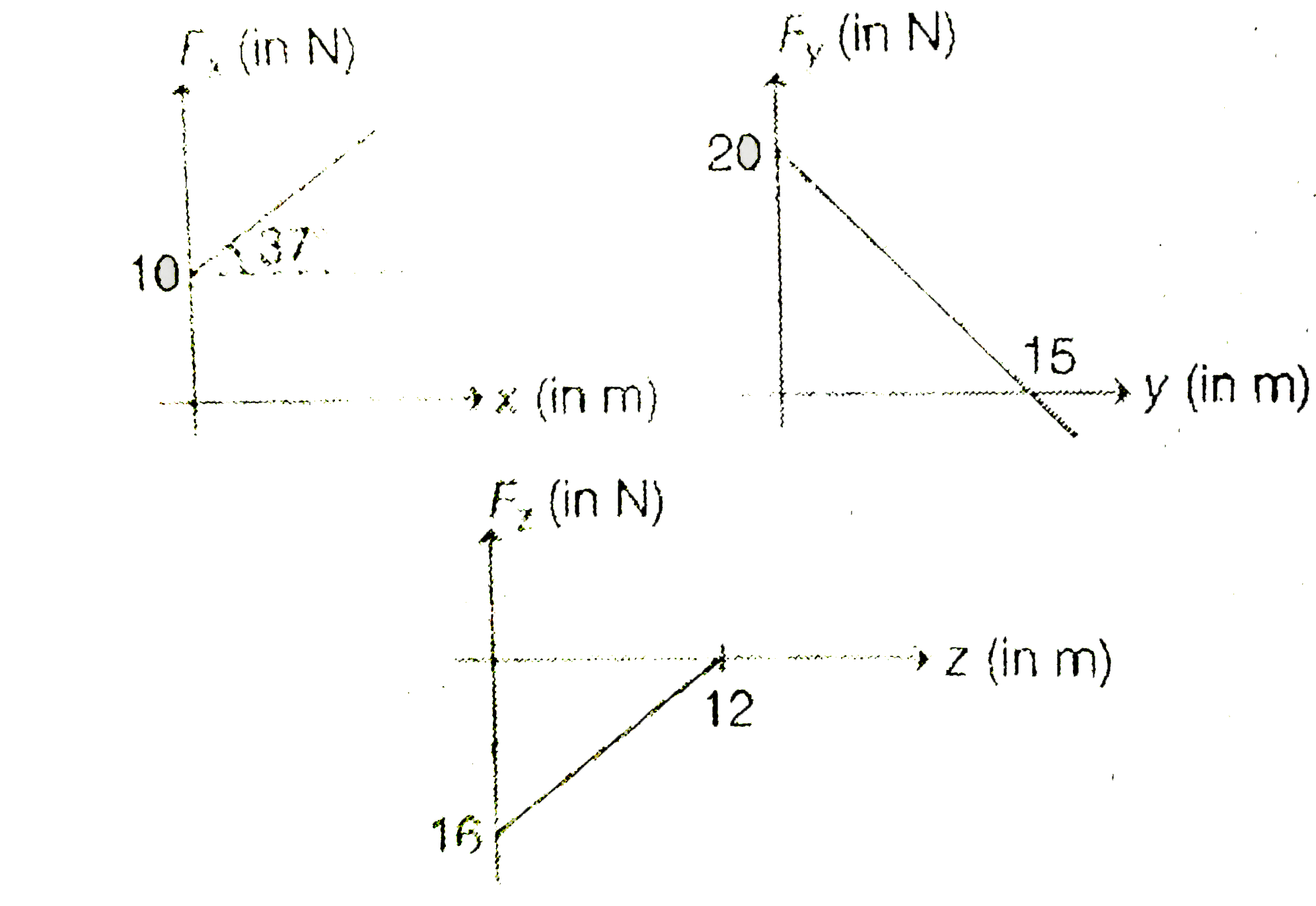
View SolutionThe magnitude of x and y components of →A are 7 and 6 respectively . Also , the magnitudes of x and y components of →A+→B are 11 and 9 respectively . Calculate the magnitude of vector →B
View SolutionThe variation of force F acting on a body moving along x - axis varies with its position (x) as shown in figure
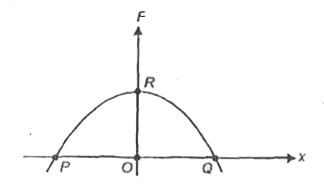
The body is in stable equilibrium stable at
View SolutionLet y=f(x) be a curve passing through (4,3) such that slope of normal at any point lying in the first quadrant is negative and the normal and tangent at any point P cuts the Y-axis at A and B respectively such that the mid-point of AB is origin, then the number of solutions of y=f(x) and f=|5−|x∣∣, is
View SolutionTwo vectors a and b have equal magnitudes of 12 units. These vectors are making angles 30°and 120° with the x axis respectively. Their sum is r . Find the x and y components of r .
View SolutionWhat displacement at an angle 60∘ to the x-axis has an x-component of 5m? ˆi and ˆj are unit vector in x and y directions, respectively.
View Solution